Mishandling Functions - Forms of Argument

Mathematical Writing - Vivaldi Franco 2014

Mishandling Functions
Forms of Argument

Many things can go wrong when we deal with functions. For instance, we may apply a function to arguments outside its domain (e.g., forming the logarithm of zero), or invert a function incorrectly (e.g., taking the wrong sign of a square root).

We begin with a proof from calculus which isn’t correct, even if it captures the essence of the argument. The chain rule for differentiating the composition of two functions states that if $$f$$ and $$g$$ are differentiable, then

$$ (g\circ f)'(x) = g'(f(x))f'(x). $$

SLOPPY PROOF. Let $$\varepsilon $$ be a real number. We compute

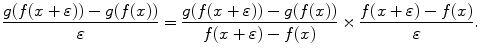
$$ \frac{g(f(x+\varepsilon ))-g(f(x))}{\varepsilon }= \frac{g(f(x+\varepsilon ))-g(f(x))}{f(x+\varepsilon ) - f(x)} \times \frac{f(x+\varepsilon )-f(x)}{\varepsilon }. $$

Letting $$\varepsilon $$ tend to zero gives the desired result. $$\square $$

The right-hand side is obtained by multiplying and dividing by $$f(x+\varepsilon )-f(x)$$. But this quantity may well be zero for non-zero $$\varepsilon $$ (e.g., if $$f$$ is constant), which invalidates the argument. A valid proof requires more delicacy.

PROOF. Let $$y=f(x)$$. Since $$g$$ is differentiable at $$y$$, we write

$$ g(y+\delta )-g(y)=g'(y)\delta +h(y,\delta )\delta $$

where $$h$$ is a continuous function with $$h(y,0)=0$$. Specialising to $$\delta =f(x+\varepsilon )-f(x)$$, we find

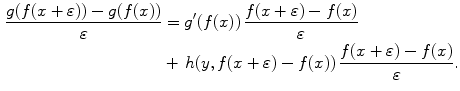
$$\begin{aligned} \frac{g(f(x+\varepsilon ))-g(f(x))}{\varepsilon }&= g'(f(x))\,\frac{f(x+\varepsilon )-f(x)}{\varepsilon }\\&+\,h(y,f(x+\varepsilon )-f(x))\,\frac{f(x+\varepsilon )-f(x)}{\varepsilon }. \end{aligned}$$

As $$\varepsilon $$ tend to zero, the last term tends to zero, being the product of a function that tends to zero and a function that tends to a finite limit (because $$f$$ is differentiable). This gives the desired result. $$\square $$

Mishandling a non-invertible function may have unpredictable consequences:

WRONG THEOREM. Every negative real number is positive.

WRONG PROOF. Let $$\alpha $$ be a negative real number. Then

$$\begin{aligned} \alpha&= -1|\alpha |=(-1)^1|\alpha |=(-1)^{2\cdot \scriptstyle \frac{1}{2}}|\alpha | =[(-1)^2]^{\frac{1}{2}}|\alpha |\\&= 1^\frac{1}{2}|\alpha |=|\alpha |>0 \end{aligned}$$

as required. $$\square $$

What’s wrong with this proof? The function $$x\mapsto x^2$$ is not invertible, and to invert it we must restrict the domain. If we restrict it to the range $$x\geqslant 0$$ and take the positive sign for the square root, then the functions $$x\mapsto x^2$$ and $$x\mapsto \sqrt{x}$$ are inverse of each other: $$x^{\scriptstyle 2\cdot \frac{1}{2}}=\sqrt{x^2}=x$$. However, if $$x$$ is negative, these functions are inverse of each other only if we take the negative sign of the square root.

Thus the error occurred in the last equality

$$ 1^\frac{1}{2}=1 $$

where, having squared a negative quantity, we mistakenly choose the positive sign of the square root. Exercise 7.3.2 deals with a more general instance of the same phenomenon.