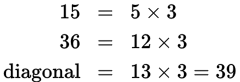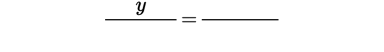PSAT/NMSQT Prep 2019 - Princeton Review 2019
Geometry
Additional topics in math
Math
CHAPTER OBJECTIVES
By the end of this chapter, you will be able to:
1. Apply the properties of lines and angles to solve geometry questions
2. Use the Pythagorean theorem, Pythagorean triplets, and special right triangles to answer questions involving triangles
3. Use concepts and theorems about congruence and similarity to solve problems about lines, angles, and triangles
4. Identify simple shapes within complex figures and use them to solve questions
5. Apply theorems about circles to find arc lengths, angle measures, chord lengths, and areas of sectors
6. Create or use an equation with two variables to solve a problem about a circle in the coordinate plane
7. Solve problems using volume formulas
SMARTPOINTS
|
Point Value |
SmartPoint Category |
|
40 Points |
Geometry |
Prepare
LINES AND ANGLES
Lines and angles are the foundation of PSAT geometry. Therefore, mastering their basic rules will make solving these questions, as well as related geometry questions, easier. With the knowledge you’ll gain from this chapter, you will be able to quickly identify geometric relationships, build upon the information given in the question, and often bypass complex algebra.
Familiarity with angle types will often unlock information that is not explicitly given in a question. This makes getting to the answer much easier for even the toughest geometry questions. First, let’s take a look at the types of angles you should be able to recognize:
|
Angle Type |
Angle Measurement |
Example |
|
Acute |
Less than 90° |
|
|
Right |
90° |
|
|
Obtuse |
Between 90° and 180° |
|
|
Straight |
180° |
|
More often than not, you’ll work with multiple angles in a single question. Therefore, it’s worth noting two likely familiar terms that involve working with two or more angles: complementary and supplementary angles. Two angles are complementary if their measures add up to 90°; if their measures add up to 180°, the angles are supplementary.
Note
Two angles need not be adjacent to be complementary or supplementary.
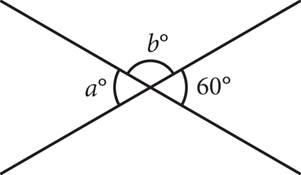
Intersecting lines create angles with special relationships you’ll need to know as well. When two lines intersect, adjacent angles are supplementary, and vertical angles (two angles opposite a vertex) are equal, or congruent. Take a look at the following figure for an example.
The angles marked a° and b° are supplementary; therefore, a + b = 180. The angle marked a° is vertical (and thus equal) to the one marked 60°, so a = 60. With this new information, you can find b: a + b = 60 + b = 180, so b = 120.
Note
Unless otherwise noted, figures on the PSAT are drawn to scale. Be especially careful when you see “Note: Figure not drawn to scale.”
When two parallel lines are intersected by another line (called a transversal), all acute angles are equal, and all obtuse angles are equal. Additionally, corresponding angles are angles that are in the same position but on different parallel lines/transversal intersections; they are also equal. Furthermore, alternate interior angles and alternate exterior angles are equal. Alternate interior angles are angles that are positioned between the two parallel lines on opposite sides of the transversal, whereas alternate exterior angles are positioned on the outside of the parallel lines on opposite sides of the transversal. Consider the following figure:
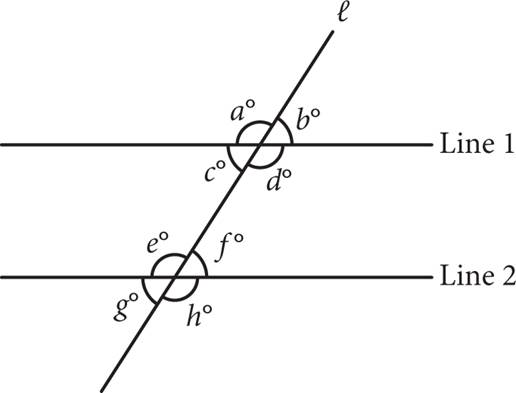
· Line 1 and Line 2 are parallel and cut by transversal ℓ.
· Angles a, d, e, and h are obtuse and equal.
· Angles b, c, f, and g are acute and equal.
· Angle pairs (b and f), (c and g), (a and e), and (d and h) are corresponding angles.
· Angle pairs (a and h) and (b and g) are alternate exterior angles.
· Angle pairs (d and e) and (c and f) are alternate interior angles.
Below is a summary of the essential theorems related to parallel lines that you’ll need to know. Notice that the converse of most of these theorems is also true.
|
Angle Theorem |
Definition |
|
Alternate Interior Angles |
|
|
Alternate Exterior Angles |
|
|
Corresponding Angles |
|
|
Vertical Angles |
|
Note
Parallel lines cut by a transversal are powerful: even if you know only one angle measure, you can get the other seven in mere seconds by knowing these rules.
TRIANGLES
Lines and angles form the basis of triangles—some of the most commonly occurring shapes on the PSAT. Luckily, triangle questions usually don’t involve a lot of complex algebra and are a great way to earn a few quick points on Test Day. Having a good command of triangle properties will help you recognize and solve these questions quickly. Many seemingly difficult questions will become easier once you can confidently speak the language of triangles.
All triangles follow the rules listed here, regardless of the type of triangle, so take the time now to get comfortable with these rules.
|
Triangle Theorem |
Definition |
|
Triangle Sum and Exterior Angle Theorems |
|
|
Isosceles Triangle Theorem |
|
|
Triangle Inequality Theorem |
|
|
Side-Angle Relationship |
|
|
Mid-Segment Theorem |
|
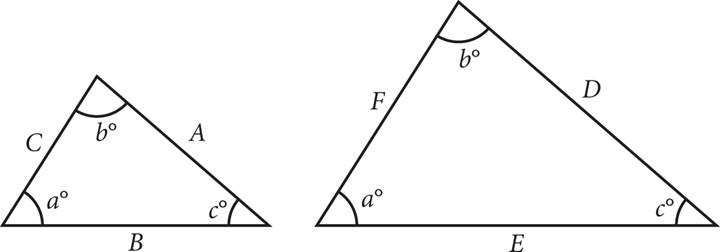
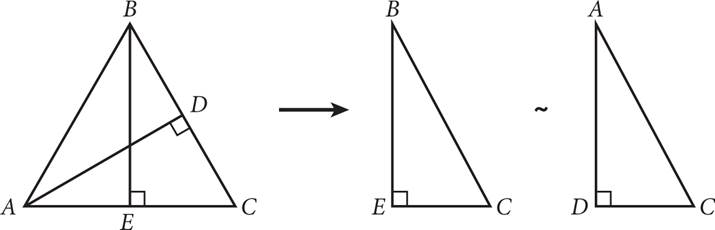
The corresponding angles and side lengths of congruent triangles are equal. Similar triangles have the same angle measurements and proportional sides. In the figure below, ΔABC and ΔDEF have the same angle measurements, so the side lengths can be set up as the following proportion: ![]() .
.
Drawing multiple heights in one triangle creates similar triangles, as shown in the diagram below. When you encounter a question like this, redrawing the similar triangles with their angles and sides in the same positions will help keep information in order.
COMPLEX FIGURES
Complex figures are also a recurring PSAT geometry topic, particularly ones that involve triangles. A complex figure is not a shape such as a dodecahedron. Instead, a complex figure is usually a larger shape that is composed of multiple (familiar) shapes; these can be obvious or cleverly hidden. These figures can always be broken down into squares, rectangles, triangles, and/or circles. No matter how convoluted the figure, following the below guidelines will lead you to the correct answer on Test Day:
· Transfer information from the question stem to the figure. If a figure isn’t provided, draw one!
· Break the figure into familiar shapes.
· Determine how one line segment can play multiple roles in a figure. For example, if a circle and triangle overlap correctly, the circle’s radius might be the triangle’s hypotenuse.
· Work from the shape with the most information to the shape with the least information.
Now use your knowledge of lines, angles, and triangles to answer a test-like question:
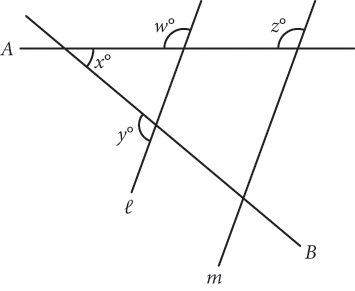
1. 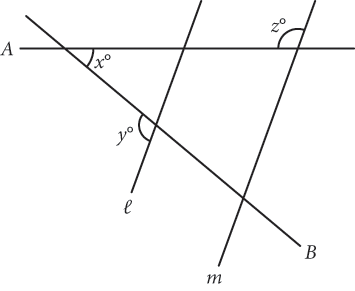
In the figure above, lines l and m are parallel and x = 40. What is the value of y + z ?
1. 220
2. 140
3. 120
4. 70
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to determine the value of y + z. |
|
|
Step 2: Choose the best strategy to answer the question Which line relationships will help you solve this question? Parallel lines are being cut by a transversal. Therefore, you know the angle where A and l intersect corresponds to the one marked z°, so they are equal. The former is labeled w° here. |
z = w |
|
A, B, and l make a triangle, which has an interior angle sum of 180°, but you’re only given one angle, x = 40. The sum of the two unknown angles of the triangle must be 140°, and because you’re looking for the sum of y and z (not y and z separately), you can just pick numbers for the triangle’s unknown angles. Suppose both are 70°. This means that the angles supplementary to these (y and w) must both be 110°. Remembering that w = z, you can substitute 110 for z as well as y. Add y and z to get 110 + 110 = 220. |
y = w = 110 y + w = y + z = 110 + 110 = 220 |
|
Step 3: Check that you answered the right question You found y + z, so you’re done. Choice (A) is correct. |
Expert Tip
The PSAT rewards students who can think flexibly about variables. If you need y + z, don’t waste time trying to find y and z individually (it’s sometimes impossible, as in this question!). Stay focused on what the question asks.
Let’s try another test-like question. Refer back to the properties and theorems as needed.
2. 
Which of the following is not true of the figure above?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
There’s no scratchwork for this question, but Kaplan’s strategic thinking is provided in the table. Follow along as we reason through the question to get the correct answer.
|
Strategic Thinking |
|
Step 1: Read the question, identifying and organizing important information as you go You need to identify the false statement. |
|
Step 2: Choose the best strategy to answer the question What does the question give you? The question stem doesn’t have information in it, but the figure gives the interior angles of a triangle. How are the side lengths and interior angles related to one another? None of the interior angles are equal, so none of the sides of the triangle are equal. Eliminate A. What theorem can you apply to choice B? The longest side of a triangle is opposite the largest angle, so arrange the angles in ascending order: 47°, 65°, 68°. The corresponding opposite sides are How can you evaluate choice (C)? Is there another way to view the relationship? The equation in (C) should look familiar; it’s a derivative of the Pythagorean theorem (square both sides to eliminate the radical). The Pythagorean theorem may be used only with right triangles, so this relationship is false. |
|
Step 3: Check that you answered the right question Choice (C) is a false statement. There is no need to check D; move on to the next question. |
THE PYTHAGOREAN THEOREM, PYTHAGOREAN TRIPLETS, AND SPECIAL RIGHT TRIANGLES
The Pythagorean theorem is one of the most fundamental equations in geometry, and it will be of great use to you on the PSAT. Common Pythagorean triplets and special right triangle ratios that originate from this formula will also serve you well on Test Day.
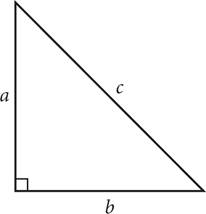
The Pythagorean theorem is an important triangle topic that you are probably familiar with already. If you know the lengths of any two sides of a right triangle, you can use the Pythagorean theorem equation to find the missing side. The equation is expressed as a2 + b2= c2, where a and b are the shorter sides of the triangle (called legs) and c is the hypotenuse, which is always across from the right angle of the triangle.
Note
The Pythagorean theorem can only be applied to right triangles.
Consider an example: A right triangle has a leg of length 9 and a hypotenuse of length 14. To find the missing leg, plug the known values into the Pythagorean theorem: 92 + b2 = 142. This simplifies to 81 + b2 = 196, which becomes b2 = 115. Take the square root of both sides to get ![]() . Because no factors of 115 are perfect squares,
. Because no factors of 115 are perfect squares, ![]() is the answer.
is the answer.
Note
Wait to simplify radicals until you have your final answer. Leave answers in radical form unless a question says otherwise or the answer choices are written as decimals.
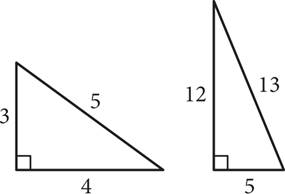
Because time is such a premium on the PSAT, time-saving strategies are invaluable, and there are two that will come in handy on triangle questions. The first is knowing common Pythagorean triplets, which are right triangles that happen to have integer sides. These triangles show up very frequently on the PSAT. The two most common are 3-4-5 and 5-12-13. Multiples of these (e.g., 6-8-10 and 10-24-26) can also pop up, so watch out for them as well. The beauty of these triplets is that if you see any two sides, you can automatically fill in the third without having to resort to the time-consuming Pythagorean theorem.
The second time-saving strategy involves recognizing special right triangles. Like Pythagorean triplets, special right triangles involve a ratio comparing the lengths of a right triangle’s legs and hypotenuse, but with these triangles, you only need to know one side in order to calculate the other two. These triangles are defined by their angles.
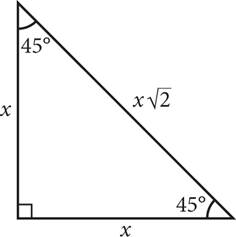
The ratio of the sides of a 45-45-90 triangle is x : x : x![]() , where x is the length of each leg and
, where x is the length of each leg and ![]() is the length of the hypotenuse.
is the length of the hypotenuse.
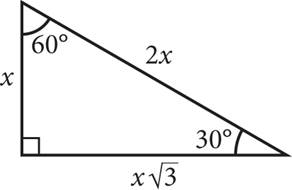
The ratio of the sides of a 30-60-90 triangle is x : x![]() : 2x, where x is the shorter leg,
: 2x, where x is the shorter leg, ![]() is the longer leg, and 2x is the hypotenuse.
is the longer leg, and 2x is the hypotenuse.
While the Pythagorean theorem can always be used to solve right triangle questions, it is not always the most efficient way to proceed. Further, many students make errors when simplifying radicals and exponents. The Pythagorean triplets and special right triangles allow you to save time and avoid those mistakes. Use them whenever possible!
Note
Although you will be given the special right triangle ratios on Test Day, you can save yourself some time by memorizing them. That way, you won’t have to keep flipping back to the formula page! You should also commit Pythagorean triplets to memory to bypass the Pythagorean theorem on Test Day.
AREA OF A TRIANGLE
On Test Day, you might also be asked to find the area of a triangle or to use the area of a triangle to find something else. The area of a triangle can be determined using ![]() , where b is the triangle base and h is the triangle height.
, where b is the triangle base and h is the triangle height.
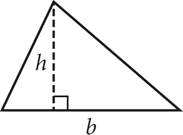
When you have a right triangle, you can use the legs as the base and the height. If the triangle isn’t a right triangle, you’ll need to draw the height in, as demonstrated in the figure shown. Remember that the height must be perpendicular to the base.
A final note about triangles: You are likely to see triangle questions involving real-world situations. But don’t fret: All you need to do is follow the Kaplan Strategy for Translating English into Math. Extract the geometry information you need, then solve!
Take a look at another test-like triangle question:
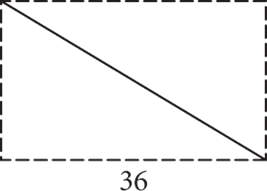
3. Owen has a rectangular field that he would like to split into two triangular fields—one for planting grain and one for planting vegetables—by building a fence from one corner of the field to the opposite corner. If the area of the field is 540 square meters and the length of the field is 36 meters, how many meters of fence will Owen need?
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to find the length of the fence (the diagonal of the rectangular field). |
|
|
Step 2: Choose the best strategy to answer the question Draw a figure to visualize the situation. Sketch the rectangle and label what you know. The area of a rectangle is the product of its length and width. Because you know the length and the area, you can find the width. |
A = 540 = 36 × w w = 540 ÷ 36 = 15 |
|
The diagonal of the rectangle is also the hypotenuse of a right triangle with legs of lengths 15 and 36. This is a multiple of the 5-12-13 Pythagorean triplet. Multiply 3 by 13 to find the length of the hypotenuse (and that of the diagonal of the rectangle). |
|
|
Step 3: Check that you answered the right question |
|
|
The question asks for the length of the fence, which is represented by the diagonal, so you’re done. Grid in 39 and move on. |
39 |
TRIANGLE CONGRUENCE THEOREMS
Many students ask why they need to learn how to do proofs when they take geometry. Although you will likely not need them in college (unless you’re a math or computer science major), there is a fundamental skill that comes with constructing proofs: the ability to construct an argument effectively for a statement or position. This skill is critical in numerous situations and fields—for criminal cases in law, research proposals in science, treatment plans in medicine, and others—so it’s a powerful tool to have in your skill set.
That being said, there’s no question that proofs can be unnerving. The good news: You will not need to construct a complete proof on the PSAT. The language of certain questions might still be slightly intimidating, but it will be far more manageable than a full-blown proof.
There are several theorems that can be used to prove two triangles are congruent; these are summarized in the following table. Make sure you are comfortable with all of them—you may need to determine that two triangles are congruent in order to find a side length or an angle measure in one or both of the triangles.
|
Triangle Congruence Theorem |
Notation |
Diagram |
|
If three sides of one triangle are congruent to the corresponding sides of another triangle, then the two triangles are congruent. |
SSS (side-side-side) |
|
|
If two sides and the included angle of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent. |
SAS (side-angle-side) |
|
|
If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent. |
AAS (angle-angle-side) |
|
|
If two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the two triangles are congruent. |
ASA (angle-side-angle) |
|
|
If the hypotenuse and leg of one right triangle are congruent to the corresponding parts of another right triangle, then the two triangles are congruent. |
HL (hypotenuse-leg) |
|
|
An angle or line segment is congruent to itself. |
Reflexive Property |
|
|
Corresponding parts of congruent triangles are congruent. |
CPCTC |
Note
There are two bogus congruence “theorems” to watch out for: AAA and SSA. Two triangles with identical angles are always similar, but they aren’t necessarily congruent. If you have two triangles with two adjacent congruent sides and a congruent angle outside them, the third side can be two different lengths. SSA is valid only with right triangles, in which case you call it HL. Never use AAA.
QUADRILATERAL THEOREMS
Quadrilaterals are four-sided figures, with interior angles that add up to 360°. You will likely not see a question solely about quadrilaterals; if a quadrilateral appears at all, it will likely contain hidden triangles. However, the properties of the quadrilateral will allow you to deduce information about the triangles present, so make sure you know the basic properties of the most common quadrilaterals.
Given the high likelihood of a Test Day geometry question containing hidden triangles, you should familiarize yourself with the types of quadrilaterals that are most likely to have useful triangles within.
|
Parallelogram Theorems |
Properties |
|
Parallelogram |
|
|
Rhombus |
|
|
Rectangle |
|
|
Square |
|
A word of caution: Do not make any assumptions about a test figure that go beyond the information provided in the question. It’s tempting to assume a quadrilateral is a rectangle or other more “friendly” shape, but unless this is proven or stated in the question (or indicated in the figure), don’t do it!
INTRODUCTION TO CIRCLES
You already know the PSAT can ask a variety of questions about lines, angles, and triangles; it can also test you on your knowledge of circles. Keep reading for a refresher on these ubiquitous shapes.
Circle Anatomy and Basic Formulas
There are a number of circle traits you should know for Test Day:
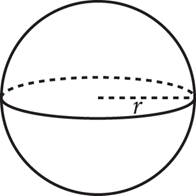
1. Radius (r): The distance from the center of a circle to its edge
2. Chord: A line segment that connects two points on a circle
3. Diameter (d): A chord that passes through the center of a circle. The diameter is always the longest chord a circle can have and is twice the length of the radius.
4. Circumference (C): The distance around a circle; the equivalent of a polygon’s perimeter. Find this using the formula C = 2πr = πd.
5. Area: The space a circle takes up, just like a polygon. A circle’s area is found by computing A = πr2.
6. Every circle contains 360°. You’ll find out more on this fact’s utility shortly.
As the formulas demonstrate, the radius is often key to unlocking several other components of a circle. Therefore, your first step for many circle questions will be to find the radius.
Circles on the Coordinate Plane and Their Equations
When you have a circle on the coordinate plane, you can describe it with an equation. The equation of a circle in standard form is as follows:
(x − h)2 + (y − k)2 = r 2
In this equation, r is the radius of the circle, and h and k are the x- and y-coordinates of the circle’s center, respectively: (h, k).
Note
A circle is one of the four conic sections, which are made by slicing a double cone with a plane. The parabola is another conic section that you read about in chapter 6. The ellipse and hyperbola (with standard forms ![]() and
and ![]() , respectively) will not be tested on the PSAT. Watch out for them in trap answer choices, however!
, respectively) will not be tested on the PSAT. Watch out for them in trap answer choices, however!
You might also see what is referred to as general form:
x 2 + y 2 + Cx + Dy + E = 0
At first glance, the general form probably doesn’t resemble the equation of a circle, but the fact that you have an x 2 term and a y 2 term with coefficients of 1 is your indicator that the equation does indeed graph as a circle. To convert to standard form, complete the square for the x terms, then repeat for the y terms. Refer to chapter 6 for a review of completing the square.
Note
The x 2 and y 2 terms in the equation of a circle occasionally have coefficients other than 1 (but the coefficients must be equal). If this is the case, simply divide all terms in the equation by the coefficient to eliminate them.
Ready to try a circle question?
4. A circle in the standard coordinate plane is given by the equation (x — 5)2 + y 2 = 38. What are the radius of the circle and the coordinates of the circle’s center?
1. radius: ![]() ; center: (−5, 0)
; center: (−5, 0)
2. radius: 19; center: (5, 0)
3. radius: 38; center: (5, 0)
4. radius: ![]() ; center: (5, 0)
; center: (5, 0)
There’s no scratchwork for this question, but Kaplan’s strategic thinking is provided in the table. Follow along as we reason through the question to get the correct answer.
|
Strategic Thinking |
|
Step 1: Read the question, identifying and organizing important information as you go You’re asked for the radius and coordinates of the center of the circle. |
|
Step 2: Choose the best strategy to answer the question What is the radius of the circle? The equation of a circle written in standard form is Where is the center of the circle? The sign in the parentheses indicates subtraction. Therefore, the x-coordinate is 5. The presence of y 2 by itself tells you that the y-coordinate is 0, because y 2 can be written as (y — 0)2, making the coordinates of the center (5, 0). Eliminate A. |
|
Step 3: Check that you answered the right question Choice (D) is the only answer that matches both pieces. |
Circle Ratios: Arcs, Central Angles, and Sectors
The PSAT can ask you about parts of circles as well. There are three partial components that can be made in a circle: arcs, central angles, and sectors. These circle pieces are frequently used in proportions with their whole counterparts, so the ability to set up ratios and proportions correctly is of utmost importance for these questions.
1. An arc is part of a circle’s circumference. Both chords and radii can cut a circle into arcs. The number of arcs present depends on how many chords and/or radii are present. If only two arcs are present, the smaller arc is called the minor arc and the larger one is the major arc. If a diameter cuts the circle in half, the two formed arcs are called semicircles. An arc length can never be greater than the circle’s circumference.
2. When radii cut a circle into multiple (but not necessarily equal) pieces, the angle at the center of the circle contained by the radii is the central angle. Because a full circle contains 360°, a central angle measure cannot be greater than this.
3. Radii splitting a circle into pieces can also create sectors, which are parts of the circle’s area. The area of a sector cannot be greater than its circle’s total area.
Here’s a summary of the ratios formed by these three parts and their whole counterparts:
![]()
Notice that all of these ratios are equal. Intuitively, this should make sense: When you slice a pizza into four equal slices, each piece should have ![]() of the cheese, sauce, crust, and toppings. If you slice a circle into four equal pieces, the same principle applies: Each piece should have
of the cheese, sauce, crust, and toppings. If you slice a circle into four equal pieces, the same principle applies: Each piece should have ![]() of the degrees, circumference, and area.
of the degrees, circumference, and area.
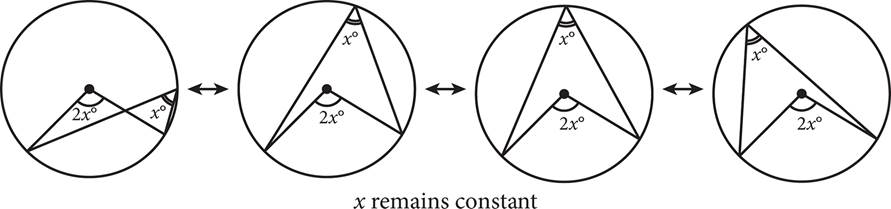
Inscribed Angle Theorem
An angle whose vertex is on the edge of the circle is called an inscribed angle. As this vertex moves along the edge, the measure of the inscribed angle remains constant as long as the minor arc created (in other words, isolated or subtended by the chords) does not change. When the chords that create an inscribed angle subtend the same minor arc that a pair of radii do, a special relationship appears: The central angle measure is twice that of the inscribed angle.
Arcs Formed Between Parallel Chords
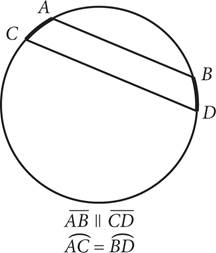
Another theorem states that two parallel chords will intercept two congruent arcs; see the following diagram for an example. The congruent arcs will be between the chords.
Tangent Lines
A tangent line touches a circle at exactly one point and is perpendicular to a circle’s radius at the point of contact. The following diagram demonstrates what this looks like:
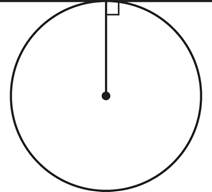
The presence of a right angle opens up the opportunity to draw otherwise hidden shapes, so pay special attention to tangents when they’re mentioned. They often come up in complex figure questions.
The next question will give you a chance to see how these properties of circles can be tested on the PSAT.
5. 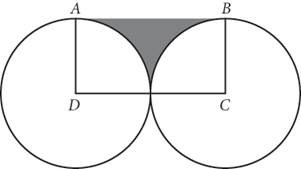
In the figure above, ABCD is a rectangle, and ![]() and
and ![]() are radii of the circles shown. If
are radii of the circles shown. If ![]() = 4, what is the perimeter of the shaded region?
= 4, what is the perimeter of the shaded region?
1. 2π + 4
2. 4π + 4
3. 4π + 8
4. 8π + 8
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go |
|
|
You must calculate the perimeter of the shaded area. |
|
|
Step 2: Choose the best strategy to answer the question |
|
|
Use your complex figure expertise to break this down. You’ll notice the top of the shaded piece is also the top of the rectangle. In addition, each curved side is an arc of one of the circles. |
perimeter comprised of a rectangle length and two circle arcs |
|
The rectangle component is easy. |
shaded area’s top = |
|
All four of the rectangle’s angles are 90°, two of which are central angles in the circles. This means the arcs are |
C = πd = 4π
P = π + π + 4 = 2π + 4 |
|
Step 3: Check that you answered the right question |
|
|
The correct answer is (A). |
INTRODUCTION TO 3-D SHAPES
Over the last several pages, you learned about two-dimensional (2-D) shapes and how to tackle PSAT questions involving them. Now you’ll learn how to do the same for questions containing three-dimensional (3-D) shapes, also called solids. There are several different types of solids that might appear on Test Day—rectangular solids, cubes, cylinders, prisms, spheres, cones, pyramids—so it is critical that you be familiar with them.
The following is a diagram showing the basic anatomy of a 3-D shape.
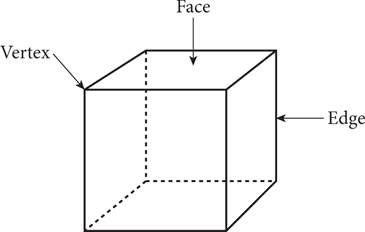
A face (or surface) is a 2-D shape that acts as one of the sides of the solid. Two faces meet at a line segment called an edge, and three faces meet at a single point called a vertex.
Keep reading for more on types of 3-D shapes and questions you could be asked about them.
Volume
Volume is the amount of 3-D space occupied by a solid. This is analogous to the area of a 2-D shape like a triangle or circle. You can find the volume of many 3-D shapes by finding the area of the base and multiplying it by the height. We’ve highlighted the base area components of the formulas in the following table using parentheses:
|
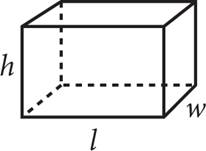
Rectangular Solid |
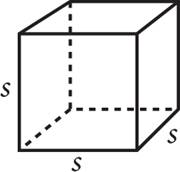
Cube |
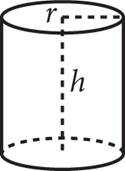
Right Cylinder |
|
|
|
|
|
(l × w) × h |
(s × s) × s = s3 |
(π × r 2) × h |
These three 3-D shapes are prisms. Almost all prisms on the PSAT are right prisms; that is, all faces are perpendicular to those with which they share edges.
Following are some examples of less commonly seen prisms:
|
Triangular Prism |
Hexagonal Prism |
Decagonal Prism |
|
|
|
|
Like the rectangular solids, cubes, and cylinders you saw earlier, these right prisms use the same general volume formula (V = Abase × h).
Note
You might not be told explicitly the area of the base of a prism, in which case you’ll need to rely on your two-dimensional geometry expertise to find it before calculating the volume.
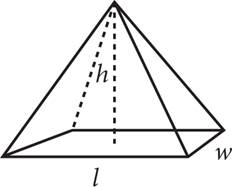
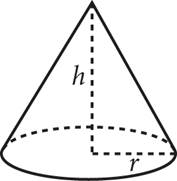
More complicated 3-D shapes include the right pyramid, right cone, and sphere. The vertex of a right pyramid or right cone will always be centered above the middle of the base. Their volume formulas are similar to those of prisms, albeit with different coefficients.
Note
Some of these formulas might look daunting, but don’t fret—you won’t have to memorize them for Test Day. They’ll be provided on the reference page at the beginning of each math section.
|
Right (Square) Pyramid |
Right Cone |
Sphere |
|
|
|
|
|
|
|
|
Note
A right pyramid can have any regular polygon as its base; the square variety is the one you’re most likely to see. Also note that the vertex above the base of a right pyramid or cone is not necessarily formed by an intersection of exactly three faces, as in prisms, but it is still a single point and is still called a vertex.
Surface Area
Surface area is the sum of the areas of all faces of a solid. You might liken this to determining the amount of wrapping paper needed to cover all faces of a solid.
To calculate the surface area of a solid, simply find the area of each face using your 2-D geometry skills, then add them all together.
Note
You won’t be expected to know the surface area formulas for right pyramids, right cones, and spheres; they’ll be provided if you need them. However, you could be asked to find the surface area of a prism, in which case you’ll be given enough information to find the area of each surface of the solid.
You might think that finding the surface area of a solid with many sides, such as a 10-sided right octagonal prism, is a tall order. However, you can save time by noticing a vital trait: This prism has two identical octagonal faces and eight identical rectangular faces. Don’t waste time finding the area of each of the 10 sides; find the area of one octagonal face and one rectangular face instead. Once complete, multiply the area of the octagonal face by 2 and the area of the rectangular face by 8, add the products together, and you’re done! The same is true for other 3-D shapes such as rectangular solids (including cubes), other right prisms, and certain pyramids.
If you’re ready to test your knowledge of 3-D shapes, check out the next question:
6. 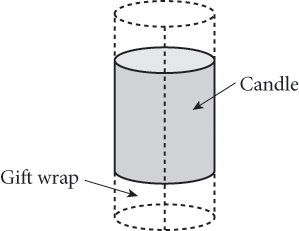
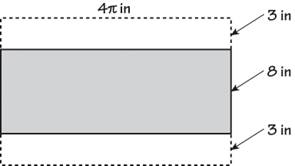
Sabine bought 10 right cylindrical candles as party favors and plans to wrap them such that the gift paper wraps around the candle height exactly once with no overlap. She wants to leave an extra 3 inches of wrapping paper past each end of the candles so she can tie both ends with a bit of ribbon. If each candle has a diameter of 4 inches and is 8 inches tall, how many square inches of wrapping paper will Sabine need to wrap one candle?
1. 32π
2. 40π
3. 56π
4. 64π
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to find the amount of wrapping paper Sabine needs to wrap one of her candles. |
|
|
Step 2: Choose the best strategy to answer the question Covering a 3-D shape (with gift wrap here) implies surface area, but be careful: One piece of gift wrap is not identical to the surface area of one of the candles because the circular top and bottom will not be covered exactly. The gift wrap will be in the shape of a rectangle. The question states that Sabine will leave extra gift wrap at both ends, so remember to take this into account. The rectangle length shares an edge with the circular top of the candle; therefore, the length is equal to the top’s circumference. |
C is rect. length, h is rect. width gift wrap for one candle: |
|
Step 3: Check that you answered the right question Nicely done! You’ve found the amount of gift wrap Sabine needs for one candle, which is (C). |
|
Practice
Now you’ll have a chance to try a few more test-like geometry questions in a scaffolded way. We’ve provided some guidance, but you’ll need to fill in the missing parts of explanations or the step-bystep math in order to get to the correct answer:
7. 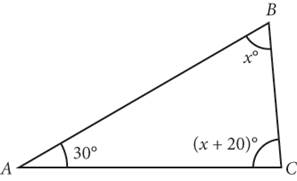
In ΔACB above, what is the measure of an angle that is supplementary to ![]() ?
?
1. 65º
2. 85º
3. 95º
4. 115º
Use the following scaffolding as your map through the question. Fill in the blanks in the table as you work from top to bottom.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to find the measure of an angle that is supplementary to |
|
|
Step 2: Choose the best strategy to answer the question Remember the rule of interior angles of a triangle: The three angles must add to 180°. Create an equation that sets the angles equal to 180. Then solve for x. Am I done? Be careful here; you are looking for the measure of an angle that is supplementary to |
supp. |
|
Step 3: Check that you answered the right question If you got (C), you are correct. |
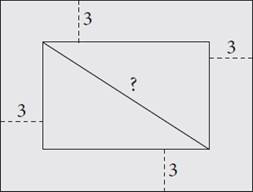
8. The size of a TV is dictated by the length of its diagonal. Whitney would like to purchase a new TV, but must first determine the maximum size TV she can mount on her living room wall. She would like a 3-inch space on each side of the TV, effectively creating a frame of empty space around the TV that is 3 inches wide on each side. If the rectangular wall space Whitney plans to use for her TV is 28.25 inches by 53 inches, what is the largest size TV (in inches) that she can fit on the wall? Round your answer to the nearest inch.
The following table can help you structure your thinking as you go about solving this problem. The Kaplan strategic thinking is provided, as are bits of structured scratchwork. If you’re not sure how to approach a question like this, start at the top and work your way down.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You’re asked for the largest size TV Whitney can mount on her wall; in other words, you need to calculate the length of its diagonal. |
|
|
Step 2: Choose the best strategy to answer the question |
|
|
First, draw a rectangle to represent the wall space. Next, draw another rectangle inside the first to represent the TV. Label the diagram with the information the question provides. Subtract the width of the empty wall space from the given dimensions. Once there, use the Pythagorean theorem to find the diagonal of the TV area, and then subtract the area of the picture from it. |
wall space: × TV space: × 2 × 2 = 2 + = |
|
Step 3: Check that you answered the right question If you got 52, you’re correct! |
9. 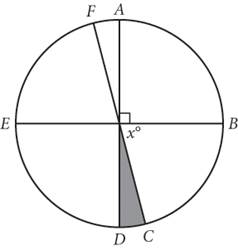
In the circle above, ![]() ,
, ![]() , and
, and ![]() are diameters. If the shaded area is equal to
are diameters. If the shaded area is equal to ![]() of the area of the circle, what is the value of x ?
of the area of the circle, what is the value of x ?

Use the scaffolding that follows as your map through the question. Fill in the blanks in the table as you work from top to bottom.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go |
|
|
You need to find the value of x. |
|
|
Step 2: Choose the best strategy to answer the question |
|
|
The shaded area is a sector for which the question has provided information. This is your cue that you should be thinking about circle proportions. |
|
|
Use degrees and sector/circle area. You know the number of degrees in a full circle, as well as the ratio of the shaded area to the entire circle area. Use a variable other than x to represent the shaded part’s central angle to avoid confusion later. |
|
|
The sector marked by A and B is 90°. Because |
x + ____ + ____ = 180 x = ____ |
|
Step 3: Check that you answered the right question |
|
|
Did you get 70? If so, you’re absolutely correct. |
10.The ratio of the lengths of the radii of two spheres is 1:2. Which of the following ratios correctly compares their volumes?
1. 1:![]()
2. 1:2
3. 1:4
4. 1:8
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go |
|
|
You need to determine the ratio of the volume of the two spheres. A ratio comparing their radii is given. |
|
|
Step 2: Choose the best strategy to answer the question Pick your own radii to make this question less abstract; just be sure they obey the given ratio. Compute the volumes of the corresponding spheres and then use the volumes to write a second ratio, reducing as necessary. |
|
|
Step 3: Check that you answered the right question |
|
|
Did you get (D)? If so, you’re absolutely correct. |
|
Perform
Now that you’ve seen the variety of ways in which the PSAT can test your geometry skills, try the following questions to check your understanding. Give yourself 5 minutes to answer the following four questions. Make sure you use the Kaplan Method for Math as often as you can. Remember, you want to emphasize speed and efficiency in addition to simply getting the correct answer.
11.ΔSNO is a triangle with vertices (0, 0), (4, 0), and (0, —3). When ΔSNO is reflected over the y-axis and then shifted up five units, Δ ICE is formed. What is the equation of the line that forms the hypotenuse of Δ ICE ?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
12.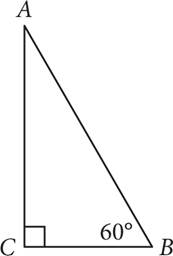
Note: Figure not drawn to scale.
If the area of ΔABC is ![]() , what is the length of
, what is the length of ![]() ?
?
1. 4
2. 6
3. 7
4. 8
13.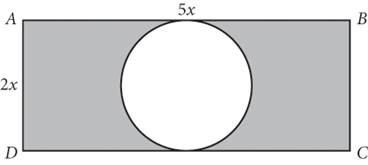
In the figure above, both ![]() and
and ![]() are tangent to the circle, and ABCD is a rectangle with side lengths 2x and 5x. What is the area of the shaded region?
are tangent to the circle, and ABCD is a rectangle with side lengths 2x and 5x. What is the area of the shaded region?
1. 10x 2 — π x 2
2. 10πx 2
3. 10x 2 — 2π x
4. 9πx 2
14.The base of a certain right square pyramid paperweight has a diagonal of length ![]() centimeters, and the paperweight’s height is 50% larger than the base edges. If the paperweight is placed inside a rectangular box full of water with dimensions of 2 cm × 4 cm × 6 cm, how many cubic centimeters of water will remain once the paperweight is completely submerged?
centimeters, and the paperweight’s height is 50% larger than the base edges. If the paperweight is placed inside a rectangular box full of water with dimensions of 2 cm × 4 cm × 6 cm, how many cubic centimeters of water will remain once the paperweight is completely submerged?

On your own
1. 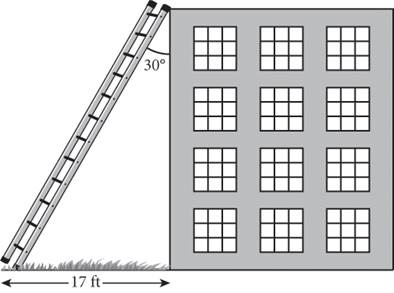
The figure above shows a ladder propped against the side of a building. If the base of the ladder is 17 feet from the building, how long in feet is the ladder?
1. 17
2. ![]()
3. ![]()
4. 34
2. 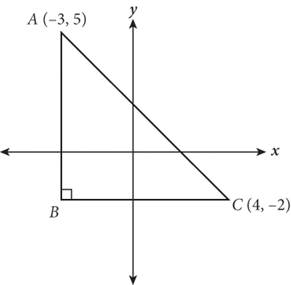
What is the measure in degrees of angle ACB in the figure above?
1. 35
2. 40
3. 45
4. 50
3. 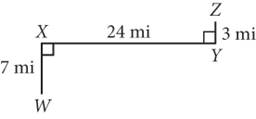
The figure above shows the route of Gina’s trip from her apartment to her gym. Gina travels 7 miles from W to X, 24 miles from X to Y, and 3 miles from Y to Z. If she were able to travel from W to Z directly, how much shorter, in miles, would the trip be?
1. 8
2. 10
3. 14
4. 26
4. 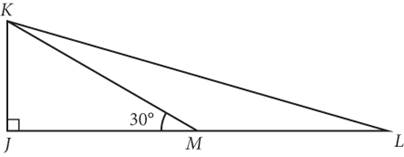
In the figure above, the length of ![]() is 2, and M is the midpoint of
is 2, and M is the midpoint of ![]() . What is the length of
. What is the length of ![]() ?
?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. The area of a right triangle is 48 square inches. If the longer leg is 4 inches more than the shorter leg, what is the length in square inches of the hypotenuse?
1. 12
2. ![]()
3. 20
4. 208
6. ΔCAT is similar to triangle ΔDOG. ΔCAT has side lengths of 7, 12, and 15. If the perimeter of ΔDOG is 51, then what is the length of its longest side?
1. 10.5
2. 15
3. 18
4. 22.5
7. ΔPQR and ΔSTU are similar triangles plotted on a coordinate plane. The vertices of ΔPQR are P(—4, 2), Q(1, 2), and R(—4, 7). If ΔSTU has vertices S(—6, —2) and T(3, —2), then what is the area in square units of ΔSTU ?

8. 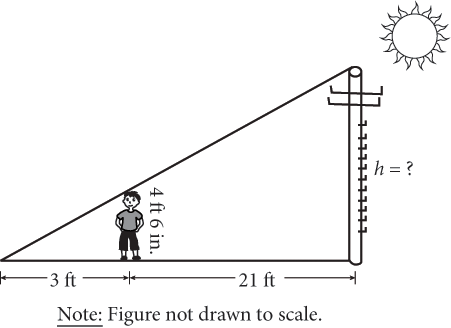
Similar triangles can be used to find the height of tall objects using shadow lengths because the sun shines on objects at the same angle. Based on the diagram above, what is the height of the telephone pole, assuming that it meets the ground at a 90° angle?

9. 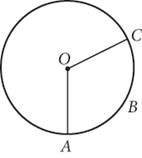
If the measure of ![]() is 100° and
is 100° and ![]() , what is the length of
, what is the length of ![]() ?
?
1. 4π
2. 5π
3. 9π
4. 18π
10.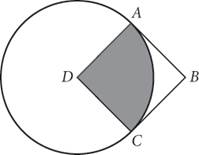
In the figure above, D is the center of the circle, and the perimeter of square ABCD is 24. What is the area of the shaded sector?
1. 9π
2. 18π
3. 24π
4. 36π
11.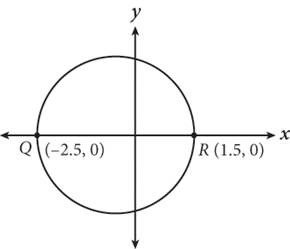
The circle shown above has diameter ![]() . Which of the following represents the equation of the circle?
. Which of the following represents the equation of the circle?
1. (x — 0.5)2 + y 2 = 4
2. (x + 0.5)2 + y 2 = 4
3. (x — 2.5)2 + (y + 1.5)2 = 0
4. (x + 2.5)2 + (y — 1.5)2 = 0
12.x 2 + y 2 + 4x − 12y = 41
What is the diameter of the circle with the equation given above?
1. 9
2. 18
3. 41
4. 81
13.Milk is poured from a full rectangular container with dimensions 4 inches by 9 inches by 10 inches into a cylindrical container with a diameter of 6 inches. Assuming the milk does not overflow the container, how many inches high will the milk reach?
1. 3π
2. 10
3. ![]()
4. 24
14.The Pyramid of Cestius in Rome serves as a tomb for Gaius Cestius, a wealthy Roman magistrate. The marble structure is a right square pyramid with a square base that stands approximately 37 meters high. If the volume of the pyramid is 11,100 cubic meters, then what is the length in meters of one side of the base?
1. 17
2. 30
3. 36
4. 45
15.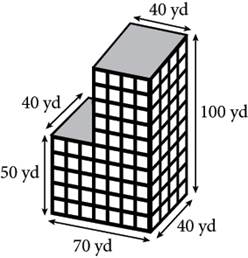
A company wants to install new air conditioners in their building. The building has the dimensions shown in the figure above. To buy the most efficient air-conditioning unit, the company needs to know the total volume of space inside the building in cubic feet. What is the volume?
1. 220,000 ft3
2. 280,000 ft3
3. 5,940,000 ft3
4. 7,560,000 ft3
16.How many units longer is the diameter of a sphere that has a volume of 36π cubic units than one with a volume of ![]() π cubic units?
π cubic units?
1. 2
2. 4
3. 5
4. 8