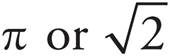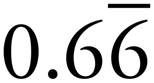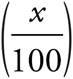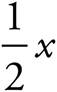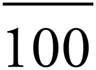SSAT & ISEE Prep 2023 - Princeton Review 2023
Fundamental math skills for the SSAT & ISEE
The basics of both tests
INTRODUCTION
Whether you are taking the Primary Level ISEE or the Upper Level SSAT, there are some basic math skills that are at the heart of many of the questions on your test. This chapter will go through the fundamental math content that you’ll see on the SSAT and ISEE, but you won’t see any SSAT or ISEE-style questions. Those are in Chapters 6 (SSAT) and 14 (ISEE). While this chapter is most relevant to those taking the Lower, Middle, or Upper Level tests, students studying for the Primary ISEE or Elementary SSAT will benefit from portions that are designated for all levels. You should go through this chapter very carefully and slowly. If you are having trouble understanding any of the content, you should ask adults for help by having them explain it more thoroughly to you. If you are taking the Middle and Upper Level tests, this chapter may serve more as a chance to review some things you may have forgotten or that you need to practice a little. Even the most difficult-seeming questions on the Upper Level exams are built on testing your knowledge of these same skills. Make sure you read the explanations and do all of the drills before going on to either the SSAT or ISEE math chapter. Answers to these drills are provided in Chapter 3.

Check out your online Student Tools for an index of where to find specific math topics in this book!
A Note to Primary 4, Lower, Elementary, and Middle Level Students
This chapter has been designed to give all students a comprehensive review of the math found on the tests. There are four sections: “The Building Blocks,” “Algebra,” “Geometry,” and “Word Problems.” At the beginnings and ends of some of these sections, you will notice information about what material you should review and what material is only for Upper Level (UL) students. Be aware that you may not be familiar with all the topics on which you will be working. If you are having difficulty understanding a topic, take this book to adults and ask that person for additional help.
A Note to Primary 2 and Primary 3 Level Students
While you will find some of the content in The Building Blocks useful, the majority of this chapter is designed for students who are in 3rd grade or older. For content that is specific to your test level, turn to the ISEE Math chapter or your online resources.
Lose Your Calculator!
You will not be allowed to use a calculator on the SSAT or the ISEE. If you have developed a habit of reaching for your calculator whenever you need to add or multiply a couple of numbers, follow our advice: put your calculator away now and take it out again after the test is behind you. Do your math homework assignments without it, and complete the practice sections of this book without it. Trust us, you’ll be glad you did.
Write It Down
Do not try to do math in your head. You are allowed to write in your test booklet if you are taking a paper-based test. You should write in your test booklet. If you are taking a computer-based test, use scratch paper. Even when you are adding just a few numbers together, write them down and do the work on paper. Writing things down not only helps to eliminate careless errors but also gives you something to refer back to if you need to double-check your work.

Write It Down; Get It Right!
You don’t get points for doing the math in your head, so don’t do it!
THE BUILDING BLOCKS
Math Vocabulary
Term |
Definition |
Examples |
Test Level |
Integer |
Any number that does not contain either a fraction or a decimal. Can be positive, negative, or zero. |
14, 3, 0, —3 |
ML, UL |
Whole number |
Positive integers and zero |
0, 1, 17 |
All |
Positive number |
Any number greater than zero |
|
ML, UL |
Negative number |
Any number less than zero |
— |
ML, UL |
Even number |
Any number that is evenly divisible by two. Note: Zero is an even number! |
—104, —2, 0, 2, 16, 104 |
All |
Odd number |
Any number that is not evenly divisible by two |
—115, —11, —1, 1, 11, 115 |
All |
Prime number |
A number that has exactly two positive factors: 1 and itself. Note: One is not a prime number, but two is. |
2, 3, 5, 7, 13, 131 |
LL, ML, UL |
Digit |
The numbers from 0 through 9 |
0, 2, 3, 7. The number 237 has digits 2, 3, and 7. |
P3, P4, EL, LL, ML, UL |
Units (ones) digit |
The digit in the ones place |
For 281, 1 is in the unit’s place. |
P3, P4, EL, LL, ML, UL |
Consecutive numbers |
Any series of numbers listed in the order they appear on the number line |
3, 4, 5 or —1, 0, 1, 2 |
All |
Distinct numbers |
Numbers that are different from one another |
2, 7, and 19 are three distinct numbers; 4 and 4 are not distinct because they are the same number. |
All |
Divisible by |
A number that can be evenly divided by another |
12 is divisible by 1, 2, 3, 4, 6, 12. |
P4, EL, LL, ML, UL |
Sum |
The result of addition |
The sum of 6 and 2 is 8 because 6 + 2 = 8. |
All |
Difference |
The result of subtraction |
The difference between 6 and 2 is 4 because 6 — 2 = 4. |
All |
Product |
The result of multiplication |
The product of 6 and 2 is 12 because 6 × 2 = 12. |
P4, EL, LL, ML, UL |
Quotient |
The result of division |
The quotient when 6 is divided by 2 is 3 because 6 ÷ 2 = 3. |
P4, EL, LL, ML, UL |
Remainder |
The amount left over when dividing |
17 ÷ 5 leaves a remainder of 2. |
EL, LL, ML, UL |
Rational number |
A number that can be written as a fraction |
|
LL, ML, UL |
Irrational number |
A number that cannot be written as a fraction |
|
UL |
Multiple |
The result of multiplying a number by an integer (not a fraction) |
40 is a multiple of 8 (8 × 5 = 40) and of 5 (5 × 8 = 40). |
ML, UL |
Factor |
Any numbers or symbols that can be multiplied together to form a product |
8 and 5 are factors of 40 because 8 × 5 = 40. |
ML, UL |
Mean (or Average) |
The result when you divide the sum of the values by the number of values |
The mean of 5 and 7 is 6 because (5 + 7) ÷ 2 = 6. |
ML, UL |
The Rules of Zero
Zero has some funny rules. Make sure you understand and remember these rules.
· Zero is neither positive nor negative.
· Zero is even.
· Zero is an integer.
· Zero multiplied by any number is zero.
· Zero divided by any number is zero.
· You cannot divide by zero (9 ÷ 0 = undefined).
The Times Table
Make sure you are comfortable with your multiplication tables up to 12. If you are having trouble with these, break out the flashcards. On one side of the card write down the multiplication problem, and on the other write down the answer. Now quiz yourself. You may also want to copy the table shown below so you can practice. For handy tips on using flashcards effectively, turn to the vocabulary chapter and read the section on flashcards.
Elementary Level
If you haven’t learned the Times Table yet, this is a great opportunity to get ahead of your classmates!
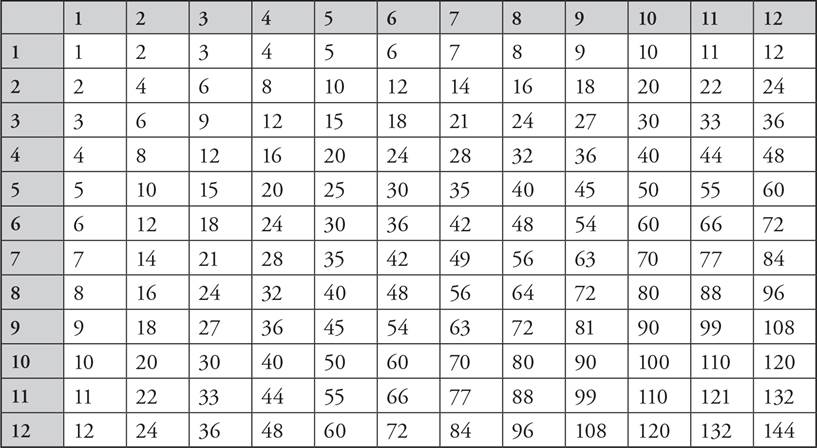

Primary level students, don’t worry about this table, you’ll learn it later.
PRACTICE DRILL 1—MATH VOCABULARY (EL, LL, ML, UL)
The following questions are for Elementary, Lower, Middle, and Upper Levels only.

Primary Level Students!
Don’t worry if you can’t do these questions. A Primary Level drill can be found online just for you. Make sure to register your book at princetonreview.com/prep for access.
1.How many integers are there between —1 and 6?
2.List three consecutive odd integers.
3.How many odd integers are there between 1 and 9?
4.What is the tens digit in the number 182.09?
5.The product of any number and the smallest positive integer is
6.What is the product of 5, 6, and 3?
7.What is the sum of 3, 11, and 16?
8.What is the difference between your answer to question 6 and your answer to question 7?
9.List three consecutive negative even integers:
10.Is 11 a prime number?
11.What is the sum of the digits in the number 5,647?
12.What is the remainder when 58 is divided by 13?
13.55 is divisible by what numbers?
14.The sum of the digits in 589 is how much greater than the sum of the digits in 1,207?
15.Is 21 divisible by the remainder of 19 ÷ 5?
16.What are the prime factors of 156?
17.What is the sum of the odd prime factors of 156?
18.12 multiplied by 3 is the same as 4 multiplied by what number?
19.What are the factors of 72?
20.How many factors of 72 are even?
How many are odd?
21.What is the mean of 6, 8, 11, and 15?

When You Are Done
Check your answers in Chapter 3, this page.
Working with Negative Numbers—Middle and Upper Levels only
It is helpful to think of numbers as having two component parts: the number itself and the sign in front of it (to the left of the number). Numbers that don’t have signs immediately to the left of them are positive. So +7 can be, and usually is, written as 7.
Adding
If the signs to the left of the numbers are the same, you add the two numbers and keep the same sign. For example:
2 + 5 = (+2) + (+5) = +7 or just plain 7
(—2) + (—5) = —7
If the signs to the left of the numbers are different, you subtract the numbers and the answer takes the sign of the larger number. For example:
5 + (—2) = 5 — 2 = 3, and because 5 is greater than 2, the answer is +3 or just plain 3.
(—2) + 5 = 5 — 2 = 3, and because 5 is greater than 2, the answer is +3 or just plain 3.
(—5) + 2 = 5 — 2 = 3, and because 5 is greater than 2, you use its sign and the answer is —3.
Subtracting
All subtraction problems can be converted to addition problems. This is because subtracting is the same as adding the opposite. “Huh?” you say—well, let’s test this out on something simple that you already know. We know that 7 — 3 = 4, so let’s turn it into an addition problem and see if we get the same answer.
7 — 3 = (+7) — (+3)
Okay, so now we reverse only the operation sign and the sign of the number we are subtracting (the second number). The first number stays the same because that’s our starting point.
(+7) + (—3)
Now use the rules for addition to solve this problem. Because the signs to the left are different, we subtract the two numbers 7 — 3 = 4, and the sign is positive because 7 is greater than 3.

This is just one way to look at subtraction problems. If you have a way that works better for you, use that!
We have just proven that subtraction problems are really just the opposite of addition problems. Now let’s see how this works in a variety of examples.
3 — 7 = (+3) — (+7) = (+3) + (—7) = 7 — 3 = 4 and, because 7 is greater than 3, the answer is —4.
—9 — 3 = (—9) — (+3) = (—9) + (—3) = —12
13 — (—5) = (+13) — (—5) = (+13) + (+5) = +18
(—5) — (—8) = (—5) + (+8) = +3
PRACTICE DRILL 2—ADDING AND SUBTRACTING NEGATIVE NUMBERS (MIDDLE/UPPER LEVELS ONLY)
1.6 + (—14) =
2.13 — 27 =
3.(—17) + 13 =
4.12 — (—15) =
5.16 + 5 =
6.34 — (+30) =
7.(—7) + (—15) =
8.(— 42) + 13 =
9.—13 — (—7) =
10.151 + (—61) =
11.(— 42) — (— 42) =
12.5 — (—24) =
13.14 + 10 =
14.(—5) + (—25) =
15.11 — 25 =

When You Are Done
Check your answers in Chapter 3, this page.
Multiplying and Dividing
The rules for multiplying and dividing positive and negative integers are so much easier to learn and use than the rules for adding and subtracting them. You simply multiply or divide as normal, and then determine the sign using the rules below.
Positive (÷ or ×) Positive = Positive
Negative (÷ or ×) Negative = Positive
Positive (÷ or ×) Negative = Negative
Negative (÷ or ×) Positive = Negative
Here are some examples.
6 ÷ 2 = 3
(—6) ÷ (—2) = 3
6 ÷ (—2) = —3
(—6) ÷ 2 = —3
2 × 6 = 12
(—2) × (—6) = 12
2 × (—6) = —12
(—2) × 6 = —12
If you are multiplying more than two numbers, simply work from left to right and deal with the numbers two at a time.
Simplify 2 × (—5) × (—10).
Step 1: multiply the first two numbers: 2 × (—5) = —10
Step 2: multiply the result with the third number: (—10) × (—10) = 100

Helpful Trick
When multiplying numbers, simply count the number of negative signs. An even number of negative signs (—6 × —3) means that the product must be a positive number. An odd number of negative signs (2 × —5) means that the product must be negative.
PRACTICE DRILL 3—MULTIPLYING AND DIVIDING NEGATIVE NUMBERS (MIDDLE/UPPER LEVEL ONLY)
1.20 ÷ (—5) =
2.(—12) × 3 =
3.(—13) × (—5) =
4.(— 44) ÷ (— 4) =
5.7 × 9 =
6.(—65) ÷ 5 =
7.(—7) × (—12) =
8.(—10) ÷ 2 =
9.81 ÷ 9 =
10.32 ÷ (—4) =
11.25 × (—3) =
12.(—24) × (—3) =
13.64 ÷ (—16) =
14.(—17) × (—2) =
15.(—55) ÷ 5 =

When You Are Done
Check your answers in Chapter 3, this page.
Order of Operations—Lower/Middle/Upper Level only
How would you attack this problem?
16 — 45 ÷ (2 + 1)2 × 4 + 5 =
To solve a problem like this, you need to know which mathematical operation to do first. The way to remember the order of operations is to use PEMDAS.

You can remember the order of operations by using the phrase below:
“Please Excuse My Dear Aunt Sally”
Now, let’s give it a try.
16 — 45 ÷ (2 + 1)2 × 4 + 5 =
1.Parentheses:
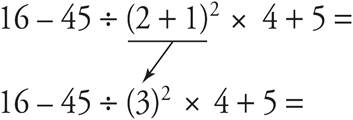
2.Exponents:
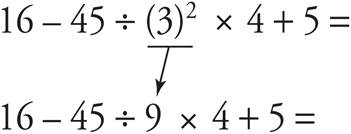
3.Multiplication and division (from left to right):
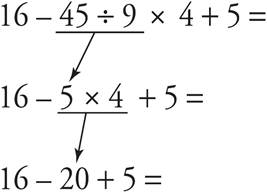
4.Addition and subtraction (from left to right):
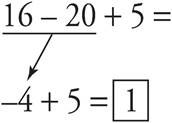
Just take it one step at a time and you’ll be able to do it in no time at all!

First Things First
Make sure you remember PEMDAS whenever you see a question with more than one operation.
PRACTICE DRILL 4—ORDER OF OPERATIONS (LOWER/MIDDLE/UPPER LEVEL ONLY)
1.10 — 3 + 2 =
2.15 + (7 — 3) — 3 =
3.3 × 2 + 3 ÷ 3 =
4.2 × (4 + 6)2 ÷ 4 =
5.420 ÷ (10 + 5 × 12) =
6.20 × 5 ÷ 10 + 20 =
7.3 + 5 × 10 × (7 — 6) ÷ 2 — 4 =
8.10 × (8 + 1) × (3 + 1) ÷ (8 — 2) =
9.12 + (5 × 2)2 — 33 ÷ 3 =
10.200 — (150 ÷ 3) × 23 =

When You Are Done
Check your answers in Chapter 3, this page.
Factors (Middle/Upper Level Only)
Factors are all the numbers that divide evenly into your original number. For example, 2 is a factor of 10; it goes in 5 times. However, 3 is not a factor of 10 because 10 divided by 3 does not produce an integer quotient (and therefore does not “go in evenly”). When asked to find the factors of a number, just make a list.
The factors of 16 are
1 and 16 (always start with 1 and the original number)
2 and 8
4 and 4
The factors of 18 are
1 and 18
2 and 9
3 and 6
Knowing some of the rules of divisibility can save you some time.
A number is divisible by |
If… |
2 |
it ends in 0, 2, 4, 6, or 8 |
3 |
the sum of the digits is divisible by 3 |
4 |
the number formed by the last two digits is divisible by 4 |
5 |
it ends in 0 or 5 |
8 |
the number formed by the last three digits is divisible by 8 |
9 |
the sum of the digits is divisible by 9 |
10 |
it ends in 0 |

Larger Factors
There’s a quick way to figure out if a number is divisible by larger numbers. Simply take the two smaller factors and check both. If a number is divisible by both 2 and 3, then it’s divisible by 6. If a number is divisible by both 3 and 4, then it’s divisible by 12.
Factor Trees (Middle/Upper Level Only)
To find the prime factors of a number, draw a factor tree.
Start by writing down the number and then drawing two branches from the number. Write down any pair of factors of that number. Now if one (or both) of the factors is not prime, draw another set of branches from that factor and write down a pair of factors for that number. Continue until you have only prime numbers at the end of your branches. Each branch end is a prime factor. Remember, 1 is NOT prime!
What are the distinct prime factors of 56? Well, let’s start with the factor tree.
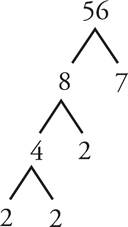
The prime factors of 56 are 2, 2, 2, and 7. Because the question asked for only the distinct prime factors, we have to eliminate the numbers that repeat, so we cross out two of the twos. The distinct prime factors of 56 are 2 and 7.
Multiples (Middle/Upper Level Only)
Multiples are the results when you multiply a number by any integer. The number 15 is a multiple of 5 because 5 times 3 equals 15. On the other hand, 18 is a multiple of 3, but not a multiple of 5. Another way to think about multiples is to consider them “counting by a number.”
The first seven positive multiples of 7 are:
7 (7 × 1)
14 (7 × 2)
21 (7 × 3)
28 (7 × 4)
35 (7 × 5)
42 (7 × 6)
49 (7 × 7)
PRACTICE DRILL 5—FACTORS AND MULTIPLES (MIDDLE/UPPER LEVEL ONLY)
1.List the first five multiples of:
2
4
5
11
2.Is 15 divisible by 3 ?
3.Is 81 divisible by 3 ?
4.Is 77 divisible by 3 ?
5.Is 23 prime?
6.Is 123 divisible by 3 ?
7.Is 123 divisible by 9 ?
8.Is 250 divisible by 2 ?
9.Is 250 divisible by 5 ?
10.Is 250 divisible by 10 ?
11.Is 10 a multiple of 2 ?
12.Is 11 a multiple of 3 ?
13.Is 2 a multiple of 8 ?
14.Is 24 a multiple of 4 ?
15.Is 27 a multiple of 6 ?
16.Is 27 a multiple of 9 ?
17.How many numbers between 1 and 50 are multiples of 6 ?
18.How many even multiples of 3 are there between 1 and 50 ?
19.How many numbers between 1 and 100 are multiples of both 3 and 4 ?
20.What is the greatest multiple of 3 that is less than 50 ?

When You Are Done
Check your answers in Chapter 3, this page.
Fractions—Primary 3 & 4, Elementary, Lower, Middle, Upper Levels
Fractions represent division. For instance, ![]() actually means five divided by eight (which equals 0.625 as a decimal).
actually means five divided by eight (which equals 0.625 as a decimal).
Another way to think of this is to imagine a pie cut into eight pieces. ![]() represents five of those eight pieces of pie.
represents five of those eight pieces of pie.
The parts of a fraction are called the numerator and the denominator. The numerator is the number on top of the fraction. It refers to the portion of the pie, while the denominator is on the bottom of the fraction and tells you how many pieces there are in the entire pie.
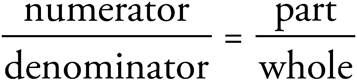
Reducing Fractions—Primary 4, Elementary, Lower, Middle, Upper Levels
Imagine a pie cut into two big pieces. You eat one of the pieces. That means that you have eaten ![]() of the pie. Now imagine the same pie cut into four pieces; you eat two. That’s
of the pie. Now imagine the same pie cut into four pieces; you eat two. That’s ![]() this time. But look, the two fractions are equivalent!
this time. But look, the two fractions are equivalent!

Remember!
As the denominator gets smaller, the value of the fraction gets bigger. After all, would you rather have ![]() of a pie or
of a pie or ![]() of one?
of one?

To reduce fractions, simply divide the top number and the bottom number by the same amount. Start out with small numbers like 2, 3, 5, or 10 and reduce again if you need to.
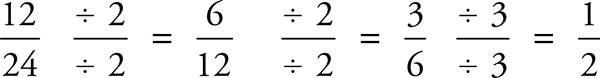
In this example, if you happened to see that both 12 and 24 are divisible by 12, then you could have saved two steps. However, don’t spend very much time looking for the largest number possible by which to reduce a fraction. Start out with a small number; doing one extra reduction doesn’t take very much time and will definitely help prevent careless errors.
PRACTICE DRILL 6—REDUCING FRACTIONS (PRIMARY 4, ELEMENTARY, LOWER, MIDDLE, UPPER)
1.![]() =
=
2.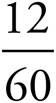 =
=
3.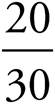 =
=
4.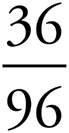 =
=
5.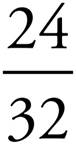 =
=
6.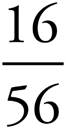 =
=
7. =
=
8. =
=
9.What does it mean when the number on top is larger than the one on the bottom?

When You Are Done
Check your answers in Chapter 3, this page.
Improper Fractions and Mixed Numbers—Lower, Middle, Upper Levels Only
Changing from Improper Fractions to Mixed Numbers
If you knew the answer to number 9 in the last drill or if you looked it up, you now know that when the number on top is greater than the number on the bottom, the fraction is greater than 1. That makes sense, because you also know that a fraction bar is really just another way of telling you to divide. So, 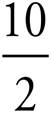 is the same as 10 ÷ 2, which equals 5, which is much greater than 1!
is the same as 10 ÷ 2, which equals 5, which is much greater than 1!

Elementary Level
You may not see this topic.
A fraction that has a greater numerator than denominator is called an improper fraction. You may be asked to change an improper fraction to a mixed number. A mixed number is an improper fraction that has been converted into a whole number and a proper fraction. To do this, let’s use 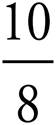 as the improper fraction that you are going to convert to a mixed number.
as the improper fraction that you are going to convert to a mixed number.
First, divide 10 by 8. This gives the whole number. 8 goes into 10 once.
Now, take the remainder, 2, and put it over the original fraction’s denominator: ![]() .
.
So the mixed number is 1![]() , or 1
, or 1![]() .
.

Put Away That Calculator!
Remember that a remainder is just the number left over after you do long division; it is not the decimal that a calculator gives you.
PRACTICE DRILL 7—CHANGING IMPROPER FRACTIONS TO MIXED NUMBERS (LOWER, MIDDLE, UPPER LEVELS ONLY)
1.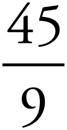 =
=
2.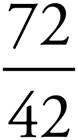 =
=
3.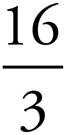 =
=
4.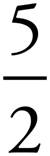 =
=
5.![]() =
=
6.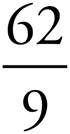 =
=
7.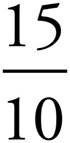 =
=
8. 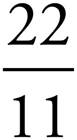 =
=
9.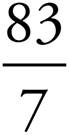 =
=
10.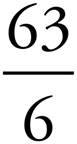 =
=

When You Are Done
Check your answers in Chapter 3, this page.
Changing Mixed Numbers to Improper Fractions
It’s important to know how to change a mixed number into an improper fraction because it may be easier to add, subtract, multiply, or divide a fraction if there is no whole number in the way. To do this, multiply the denominator by the whole number and then add the result to the numerator. Then put this sum on top of the original denominator. For example:
1![]()
Multiply the denominator by the whole number: 2 × 1 = 2
Add this to the numerator: 2 + 1 = 3
Put this result over the original denominator: ![]()
1![]() =
= ![]()
PRACTICE DRILL 8—CHANGING MIXED NUMBERS TO IMPROPER FRACTIONS (LOWER, MIDDLE, UPPER LEVELS ONLY)
1.6![]() =
=
2.2![]() =
=
3.23![]() =
=
4.6![]() =
=
5.7![]() =
=
6.7![]() =
=
7.10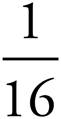 =
=
8.5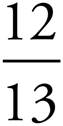 =
=
9.4![]() =
=
10.33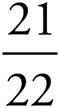 =
=

When You Are Done
Check your answers in Chapter 3, this page.
Adding and Subtracting Fractions with a Common Denominator—Lower, Middle, Upper Levels only
To add or subtract fractions with a common denominator, just add or subtract the top numbers and leave the bottom numbers alone.
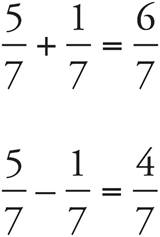
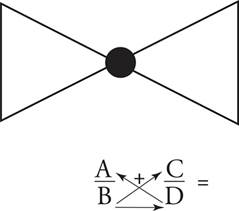
Adding and Subtracting Fractions When the Denominators Are Different—Lower, Middle, Upper Levels only
In the past, you have probably tried to find common denominators so that you could just add or subtract straight across. There is a different way; it is called the Bowtie.

No More “Least Common Denominators”
Using the Bowtie to add and subtract fractions eliminates the need for the least common denominator, but you may need to reduce the result.
This diagram may make the Bowtie look complicated. It’s not. There are three steps to adding and subtracting fractions.
Step 1: Multiply diagonally going up.
First B × C. Write the product next to C.
Then D × A. Write the product next to A.
Step 2: Multiply straight across the bottom, B × D.
Write the product as the denominator in your answer.
Step 3: To add, add the numbers written next to A and C.
Write the sum as the numerator in your answer.
To subtract, subtract the numbers written next to A and C. Write the difference as the numerator in your answer.
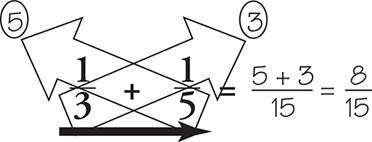
PRACTICE DRILL 9—ADDING AND SUBTRACTING FRACTIONS (LOWER, MIDDLE, UPPER LEVELS ONLY)
1. 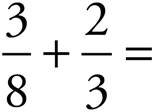
2. 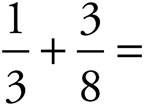
3. 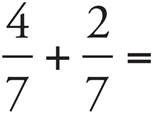
4. 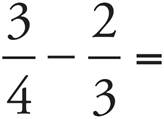
5. 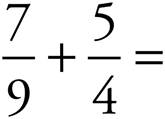
6. 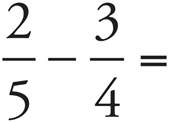
7. 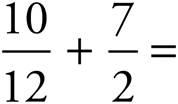
8. 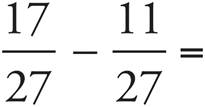
9. 
UPPER LEVEL ONLY
10. 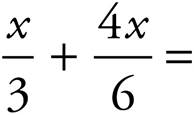
11. 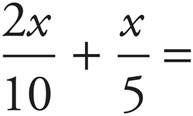
12. 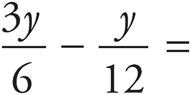

When You Are Done
Check your answers in Chapter 3, this page.
Multiplying Fractions—Middle and Upper Levels only
Multiplying can be a pretty simple thing to do with fractions. All you need to do is multiply straight across the tops and bottoms.
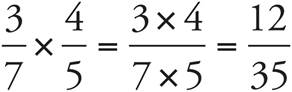
Dividing Fractions—Middle and Upper Levels only
Dividing fractions is almost as simple as multiplying. You just have to flip the second fraction and then multiply.
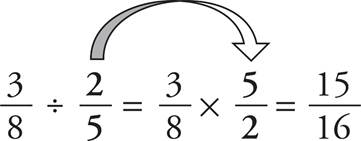
Dividing fractions can be easy as pie; just flip the second fraction and multiply.
Remember Reciprocals?
A reciprocal results when you flip a fraction—that is, exchange the numerator and the denominator. So the reciprocal of ![]() is what? Yep, that’s right:
is what? Yep, that’s right: ![]() .
.
PRACTICE DRILL 10—MULTIPLYING AND DIVIDING FRACTIONS (MIDDLE AND UPPER LEVELS ONLY)
1. 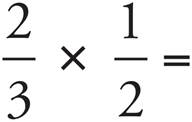
2. 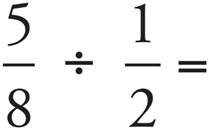
3. 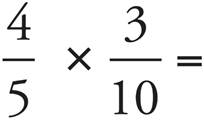
4. 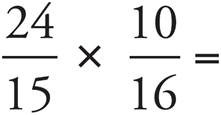
5. 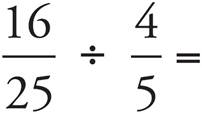

When You Are Done
Check your answers in Chapter 3, this page.
Decimals—Lower, Middle, Upper Levels only
Remember, decimals and fractions are just two different ways of writing the same thing.
Be sure you know the names of all the decimal places. Here’s a quick reminder.
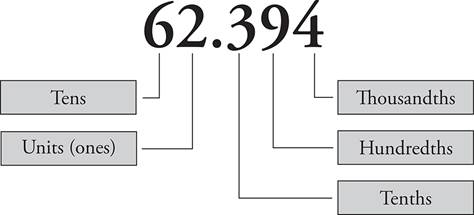
Adding Decimals
To add decimals, just line up the decimal places and add.
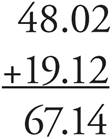
Subtracting Decimals
To subtract, do the same thing. Line up the decimal places and subtract.
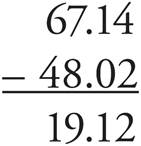
Multiplying Decimals—Middle and Upper Levels only
To multiply decimals, first count the number of digits to the right of the decimal point in the numbers you are multiplying. Then, multiply and, on the product, count that same number of spaces from right to left—this is where you put the decimal point.
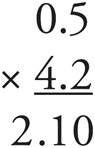
2.10 (two digits to the right of the decimal point)
Dividing Decimals—Middle and Upper Levels only
To divide, move the decimal points in both numbers the same number of spaces to the right until you are working with an integer in the divisor.
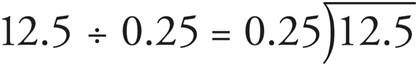
Now move both decimals over two places and solve the problem.
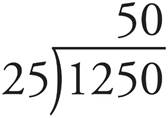
And you’re done! Remember: you do not put the decimals back into the problem.
PRACTICE DRILL 11—DECIMALS
1.1.43 + 17.27 =
2.2.49 + 1.7 =
Lower/Middle/Upper Levels
3.7 — 2.038 =
Middle/Upper Levels only
4.4.25 × 2.5 =
5.0.02 × 0.90 =
6.180 ÷ 0.03 =
7.0.10 ÷ 0.02 =

When You Are Done
Check your answers in Chapter 3, this page.
Converting Fractions to Decimals and Back Again
From Fractions to Decimals
As we learned when we introduced fractions a little earlier, a fraction bar is just a division sign.
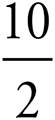 is the same as 10 ÷ 2, or 5
is the same as 10 ÷ 2, or 5
In the same sense:
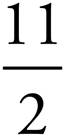 = 1 ÷ 2, or 0.5
= 1 ÷ 2, or 0.5
In fact, we can convert any fraction to its decimal equivalent by dividing the top number by the bottom number:
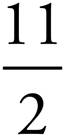 = 11 ÷ 2 = 5.5
= 11 ÷ 2 = 5.5
From Decimals to Fractions
To change a decimal to a fraction, look at the digit furthest to the right. Determine what place that digit is in (e.g., tenths, hundredths, and so on) and then put the decimal (without the decimal point) over that number (e.g., 10, 100, and so on). Let’s change 0.5 into a fraction.
5 is in the tenths place, so we put it over 10.
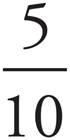 reduces to
reduces to 
PRACTICE DRILL 12—CONVERTING FRACTIONS TO DECIMALS AND BACK AGAIN (LOWER/MIDDLE/UPPER LEVELS)
Fill in the table below by converting the fractions to decimals, and vice versa. The fractions and decimals in this table are those most often tested on the SSAT and ISEE, so memorize them now and save yourself time later.
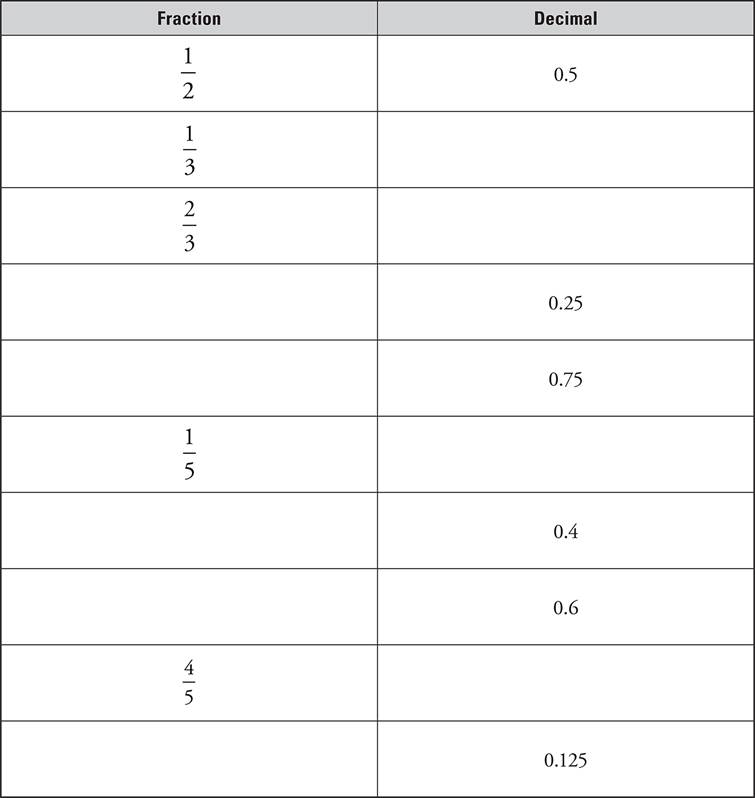

When You Are Done
Check your answers in Chapter 3, this page.
Percents—Middle and Upper Levels only
Percentages are an extension of fractions. Let’s go back to that pie we were talking about in the section on fractions. Let’s say we had a pie that was cut into four equal pieces. If you ate one piece of the pie, then we could say that the fractional part of the pie that you have eaten is:
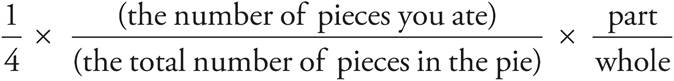
Now let’s find out what percentage of the pie you have eaten. Percent literally means “out of 100.” When we find a percent, we are really trying to see how many times out of 100 something happens. To determine the percent, you simply take the fractional part and multiply it by 100.
![]() × 100 =
× 100 = 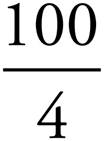 = 25%
= 25%
You’ve probably seen percents as grades on your tests in school. What does it mean to get 100% on a test? It means you got every question correct. Let’s say you got 25 questions right out of a total of 25. So we put the number of questions you got right over the total number of questions and multiply by 100.
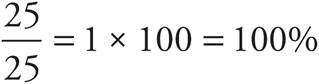
Let’s says that your friend didn’t do as well on this same test. He answered 20 questions correctly. Let’s figure out the percentage of questions he got right.
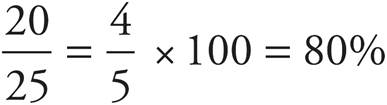
What percentage did he get wrong?
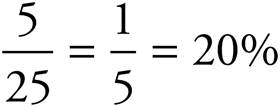
Notice that the percentage of questions he got right (80%) plus the percentage of questions he got wrong (20%) equals 100%.
PRACTICE DRILL 13—PERCENTS (MIDDLE/UPPER LEVELS)
1.A bag of candies contains 15 butterscotches, 20 caramels, 5 peppermints, and 10 toffees.
a) The butterscotches make up what percentage of the candies?
b) The caramels?
c) The peppermints?
d) The toffees?
2.A student answered 75% of the questions on a test correctly and left 7% of the questions blank. What percentage of the questions did the student answer incorrectly?
3.Stephanie’s closet contains 40 pairs of shoes. She has 8 pairs of sneakers, 12 sets of sandals, 16 pairs of boots, and the rest are high heels.
a) What percentage of the shoes are sneakers?
b) Sandals?
c) Boots?
d) High heels?
e) How many high heels does Stephanie own?
4.A recipe for fruit punch calls for 4 cups of apple juice, 2 cups of cranberry juice, 3 cups of grape juice, and 1 cup of seltzer. What percentage of the punch is juice?
5.Five friends are chipping in for a birthday gift for their teacher. David and Jakob each contribute $13. Stephanie, Kate, and Janice each contribute $8.
a) What percentage of the total did the girls contribute?
b) What percentage of the total did the boys contribute?

When You Are Done
Check your answers in Chapter 3, this page.
More Percents—Middle and Upper Levels Only
Another place you may have encountered percents is at the shopping mall. Stores offer special discounts on their merchandise to entice shoppers to buy more stuff. Most of these stores discount their merchandise by a certain percentage. For example, you may see a $16 shirt that is marked 25% off the regular price. What does that mean?
Percents are not “real” numbers. In the above scenario, the shirt was not $25 less than the regular price (then they’d have to pay you money!), but 25% less. So how do you figure out how much that shirt really costs and how much money you are saving?
To find how much a percent is in “real” numbers, you need to first take the percent and change it to a fraction.
Because percent means “out of 100,” to change a percent to a fraction, simply put the percent over 100.
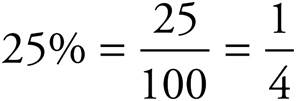
Now let’s get back to that shirt. Multiply the regular price of the shirt, $16, by the fraction.
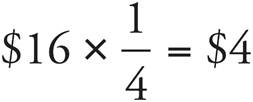
This means 25% of 16 is $4. You get $4 off the original price of the shirt. If you subtract that from the original price, you find that the new sale price is $12.
Guess what percentage the sale price is of the regular price? If you said 75 percent, you’d be right!

Tip:
Changing a decimal to a percent is the same as changing a fraction to a percent. Multiply the decimal by 100 (move the decimal two spaces to the right). So 0.25 as a percent is 0.25 × 100 = 25%.
PRACTICE DRILL 14—MORE PERCENTS (MIDDLE/UPPER LEVELS)
Fill in the missing information in the table below.
Fraction |
Decimal |
Percent |
|
0.5 |
0.5 |
|
||
|
||
25% |
||
0.75 |
||
|
||
40% |
||
0.6 |
||
|
||
12.5% |
1.25% of 84 =
2.33![]() % of 27 =
% of 27 =
3.20% of 75 =
4.17% of 300 =
5.16% of 10% of 500 =
6.A dress is marked down 15% from its regular price. If the regular price is $120, what is the sale price of the dress? The sale price is what percentage of the regular price of the dress?

Tip:
The word of in word problems means multiply!
7.Steve goes to school 80% of the 365 days of the year. How many days does Steve go to school?
8.Jennifer answered all 36 questions on her history test. If she got 25% of the questions wrong, how many questions did she get right?
9.During a special one-day sale, the price of a television was marked down 20% from its original price of $100. Later that day, the television was marked down an additional 10%. What was the final sale price?

When You Are Done
Check your answers in Chapter 3, this page.
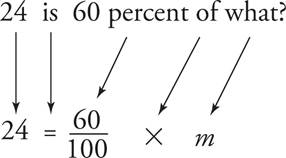
Percent Change—Upper Level Only
There is one special kind of percent question that shows up on the SSAT and ISEE: percent change. This type of question asks you to find by what percent something has increased or decreased. Instead of taking the part and dividing it by the whole, you will take the difference between the two numbers and divide it by the original number. Then, to turn the fraction to a percent, divide the numerator by the denominator and multiply by 100.
For example:
The number of people who streamed Umbrella Academy in its second season was 3,600,000. During the first season, only 3,000,000 streamed the show. By approximately what percent did the audience increase?
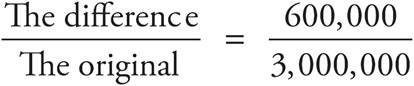
(The difference is 3,600,000 — 3,000,000.)
The fraction reduces to ![]() , and
, and ![]() as a percent is 20%.
as a percent is 20%.
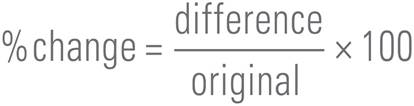
PRACTICE DRILL 15—PERCENT CHANGE (UPPER LEVEL ONLY)
1.During a severe winter in Ontario, the temperature dropped suddenly to 10 degrees below zero. If the temperature in Ontario before this cold spell occurred was 10 degrees above zero, by what percent did the temperature drop?
2.Primo Burger wants to attract more customers by increasing the size of its patties. From now on Primo’s patties are going to be 4 ounces larger than before. If the size of its new patty is 16 ounces, by approximately what percent has the patty increased?

When You Are Done
Check your answers in Chapter 3, this page.
BASIC EXPONENTS—MIDDLE AND UPPER LEVELS ONLY
Exponents are just another way to indicate multiplication. For instance, 32 simply means to multiply three by itself two times, so 32 = 3 × 3 = 9. If you remember that rule, even higher exponents won’t seem very complicated. For example:
25 = 2 × 2 × 2 × 2 × 2 = 32
The questions on the SSAT and ISEE don’t generally use exponents higher than four or five, so this is likely to be as complicated as it gets.
The rule for exponents is simple: when in doubt, write it out! Don’t try to figure out two times two times two times two times two in your head (just look at how silly it looks written down using words!). Instead, write it as a math problem and just work through it one step at a time.
When in Doubt, Write It Out!
Don’t try to compute exponents in your head. Write them out and multiply!
What would you do if you were asked to solve this problem?
Q3 × Q2 =
Let’s look at this one carefully. Q3 means Q × Q × Q and Q2 means Q × Q. Put them together and you’ve got:
(Q × Q × Q) × (Q × Q) =
How many Q’s is that? Count them. Five! The answer is Q5. Be careful when multiplying exponents like this so that you don’t get confused and multiply the actual exponents, which would give you Q6. If you are ever unsure, don’t spend a second worrying; just write out the exponent and count the number of things you are multiplying.
Basic Roots—(Middle and Upper Levels Only)
A square root (also called a “radical expression”) is just the “undoing” of squaring a number. 22 = 2 × 2 or 4, so the square root of 4 is 2.
You will see square roots written this way on tests: 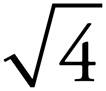 .
.
Use the Times Table on this page to make flashcards of the first 12 perfect squares and their square roots.
For example, since 4 x 4 = 16, that means 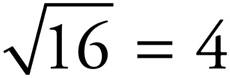 . Write
. Write 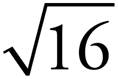 on one side of your flashcard and 4 on the other side.
on one side of your flashcard and 4 on the other side.
Cube roots and other larger roots work the same way as square roots - they “undo” exponents. So since 23 = 2 x 2 x 2 = 8, that means 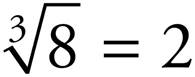 .
.
PRACTICE DRILL 16—BASIC EXPONENTS AND SQUARE ROOTS (MIDDLE AND UPPER LEVELS ONLY)
1.23 =
2.24 =
3.33 =
4.43 =
5.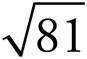 =
=
6.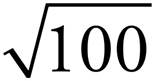 =
=
7.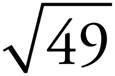 =
=
7.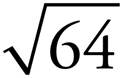 =
=
9.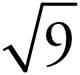 =
=
10.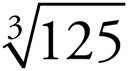 =
=
11.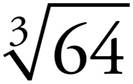 =
=
12.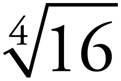 =
=

When You Are Done
Check your answers in Chapter 3, this page.
Advanced Exponents—Upper Level Only
Adding and Subtracting with Exponents
When adding or subtracting expressions with exponents, the bases and exponents have to match. 32 + 32 = 2(32) When a variable is involved, the bases and exponents have to match, and you’ll just add or subtract the coefficients (the number to the left of the variable): 9x2 — 4x2 = 5x2
Multiplying and Dividing Exponents with the Same Base
You can multiply and divide exponents with the same base without having to expand out and calculate the value of each exponent. The bottom number, the one you are multiplying, is called the base. (However, note that to multiply 23 × 52 you must calculate the value of each exponent separately and then multiply the results. That’s because the bases are different.)

For exponents with the same base, remember MADSPM:
When you Multiply with exponents, Add them. When you Divide with exponents, Subtract. When you see Powers with exponents, Multiply.
Exponents can ONLY be combined when the expression involves multiplication or division. Pay attention to the operation that is used in the problem when dealing with exponents!
To multiply, add the exponents.
23 × 24 = 23+4 = 27
To divide, subtract the exponents.
28 ÷ 25 = 28—5 = 23
To take an exponent to another power, multiply the exponents.
(23)3 = 23×3 = 29
Anything raised to the first power is itself:
31 = 3 x1 = x
Anything raised to the 0 power is 1:
30 = 1 x0 = 1
Negative exponents mean reciprocal: flip it over and get rid of the negative sign in the exponent.
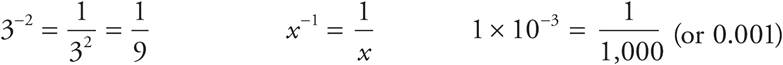
Advanced Square Roots - Upper Level Only
Sometimes you’ll be given square roots in which the number under the root sign is not a perfect square. When that’s the case, factor the number under the square root sign and separate into two separate square roots. To simplify 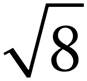 , first factor 8 into 4 and 2.
, first factor 8 into 4 and 2. 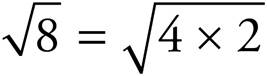 . When there’s multiplication or division under the square root sign, the operation can be broken apart into separate roots:
. When there’s multiplication or division under the square root sign, the operation can be broken apart into separate roots: 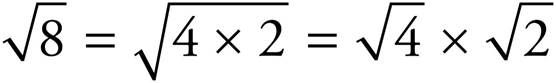 . Now simplify the square root of the perfect square.
. Now simplify the square root of the perfect square. 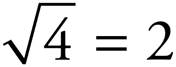 , so
, so 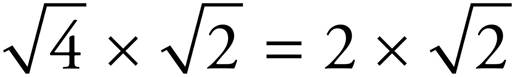 , which is written as
, which is written as 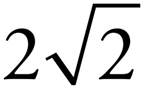 .
.
This also works in the opposite direction. When multiplying or dividing, the numbers under two (or more) radical signs can be combined.
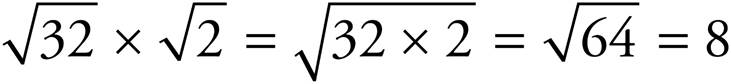
Always be on the lookout for perfect squares as “hidden” factors or multiples of the numbers you’re given! In order to add or subtract radical expressions, the number under the radical sign must be the same and you’ll add or subtract the coefficients.
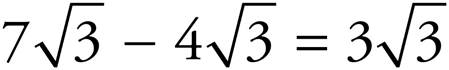
You may need to simplify the radical expression before adding or subtracting:
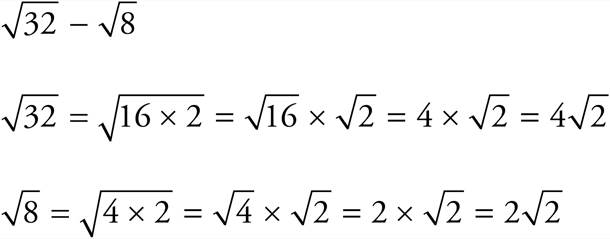
Now that the numbers under the radical sign match, subtract the coefficients:
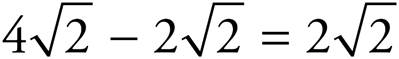
PRACTICE DRILL 17—ADVANCED EXPONENTS & ROOTS (UPPER LEVEL ONLY)
Simplify each expression.
1. 35 × 33 =
2. 72 × 77 =
3. 53 × 54 =
4. 1523 ÷ 1520 =
5. 413 ÷ 44 =
6. 1010 ÷ 106 =
7. (53)6 =
8. (812)3 =
9. (95)5 =
10. (22)14 =
11. 34 + 34 =
12. 7x6 — 3x6 =
13. 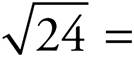
14. 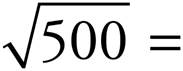
15. 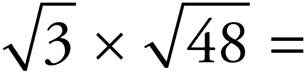
16. 
17. 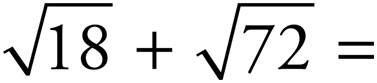
18. 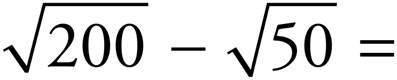

When You Are Done
Check your answers in Chapter 3, this page.
REVIEW DRILL 1—THE BUILDING BLOCKS
1. Is 1 a prime number?
2. How many factors does 100 have?
3. —10 + (—20) =
4. 100 + 50 ÷ 5 × 4 =
5. 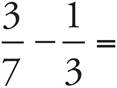
6. 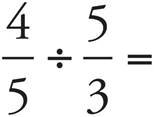
7. 1.2 × 3.4 =
8. 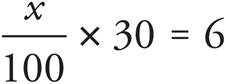 . Find the value of x.
. Find the value of x.
9. 15 =
10. 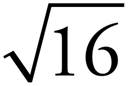 =
=
11. What are the first 10 perfect squares?

When You Are Done
Check your answers in Chapter 3, this page.
ALGEBRA—ELEMENTARY, LOWER, MIDDLE, AND UPPER LEVELS ONLY
An Introduction
If you’re a Lower Level, Elementary Level, or Middle Level student, you may not yet have begun learning about algebra in school, but don’t let that throw you. If you know how to add, subtract, multiply, and divide, you can solve an algebraic equation. Lower and Elementary Level students need to understand only the section below titled “Solving Simple Equations.” Middle Level students should complete all of the “Solving Simple Equations” drills and as much of the Upper Level material as possible. Upper Level students need to go through the entire Algebra section carefully to make sure they can solve each of the question types.
Solving Simple Equations
Algebraic equations involve the same basic operations that you’ve dealt with throughout this chapter, but instead of using only numbers, these equations use a combination of numbers and letters. These letters are called variables. Here are some basic rules about working with variables that you need to understand.
· A variable (usually x, y, or z) replaces an unknown number in an algebraic equation.
· It is usually your job to figure out what that unknown number is.
· If a variable appears more than once in an equation, that variable is always replacing the same number.
· When a variable is directly to the right of a number, with no sign in between them, the operation that is holding them together is multiplication (e.g., 3y = 3 × y).
· You can add and subtract like variables (e.g., 2z + 5z = 7z).
· You cannot add or subtract unlike variables (e.g., 2z and 3y cannot be combined).
To solve simple algebraic equations, you need to think abstractly about the equation. Let’s try one.
2 + x = 7
What does x equal?
Well, what number plus 2 gives you 7? If you said 5, you were right and x = 5.
2y = 16
In the first equation, we subtracted 2 from both sides. In the second equation, we divided both sides by 2.
What does y equal?
Now you need to ask yourself what multiplied by 2 gives you 16. If you said 8, you were right! y = 8.
Tip: You can check to see if you found the right number for the variable by replacing the variable in the equation with the number you found. So in the last problem, if we replace y with 8 and rewrite the problem, we get 2 × 8 = 16. And that’s true, so we got it right!
PRACTICE DRILL 18—SOLVING SIMPLE EQUATIONS (LOWER, ELEMENTARY, MIDDLE, AND UPPER LEVELS)
1.If 35 — x = 23, then x =
2.If y + 12 = 27, then y =
3.If z — 7 = 21, then z =
4.If 5x = 25, then x =
5.If 18 ÷ x = 6, then x =
6.If 3x = 33, then x =
7.If 65 ÷ y = 13, then y =
8.If 14 = 17 — z, then z =
9.If ![]() y = 24, then y =
y = 24, then y =
10.If 136 + z = 207, then z =
11.If 7x = 84, then x =
12.If y ÷ 2 = 6, then y =
13.If z ÷ 3 = 15, then z =
14.If 14 + x = 32, then x =
15.If 53 — y = 24, then y =

When You Are Done
Check your answers in Chapter 3, this page.
Manipulating an Equation—Middle and Upper Levels Only
To solve an equation, your goal is to isolate the variable, meaning that you want to get the variable on one side of the equation and everything else on the other side.
3x + 5 = 17
To solve this equation, follow these two steps.
Step 1: Move elements around using addition and subtraction. Get variables on one side and numbers on the other. Simplify.
Step 2: Divide both sides of the equation by the coefficient, the number in front of the variable. If that number is a fraction, multiply everything by the denominator.
For example:

Remember: Whatever you do to one side, you must also do to the other.
Taking Sides
You can do anything you want to one side of the equation, as long as you make sure to do exactly the same thing to the other side.
PRACTICE DRILL 19—MANIPULATING AN EQUATION (MIDDLE AND UPPER LEVELS ONLY)
1.If 8 = 11 — x, then x =
2.If 4x = 20, then x =
3.If 5x — 20 = 10, then x =
4.If 4x + 3 = 31, then x =
5.If m + 5 = 3m — 3, then m =
6.If 2.5x = 20, then x =
7.If 0.2x + 2 = 3.6, then x =
8.If 6 = 8x + 4, then x =
9.If 3(x + y) = 21, then x + y =
10.If 3x + 3y = 21, then x + y =
11.If 100 — 5y = 65, then y =

When You Are Done
Check your answers in Chapter 3, this page.
Manipulating Inequalities—Middle and Upper Levels Only
Manipulating an inequality is just like manipulating an equation that has an equals sign, except for one rule: if you multiply or divide by a negative number, flip the inequality sign.
Helpful Trick
Think of the inequality sign as an alligator, and the alligator always eats the bigger meal.
Let’s try an example.
—3x < 6
Divide both sides by —3, and then flip the inequality sign.
x > —2
PRACTICE DRILL 20—MANIPULATING INEQUALITIES (MIDDLE AND UPPER LEVELS ONLY)
Solve for x.
1.4x > 16
2.13 — x > 15
3.15x — 20x < 25
4.12 + 2x > 24 — x
5.7 < —14 — 3x

When You Are Done
Check your answers in Chapter 3, this page.
Functions—Middle and Upper Levels Only
In a function problem, an arithmetic operation is defined and then you are asked to perform it on a number. A function is just a set of instructions written in a strange way.
The function # is defined as x = 3x(x + 1)
On the left there is usually a variable with a strange symbol next to or around it.
In the middle is an equals sign.
On the right are the instructions. These tell you what to do with the variable.
What follows will be a question that asks you the value of the expression when the variable is a particular number.
What does #5 equal?
#5 = (3 × 5)(5 + 1) Just replace each x with a 5!
Here, the function (indicated by the # sign) simply tells you to substitute a 5 wherever there was an x in the original set of instructions. Functions look confusing because of the strange symbols, but once you know what to do with them, they are just like manipulating an equation.
Sometimes more than one question will refer to the same function. The following drill, for example, contains multiple questions about one function. In cases such as this, the first question tends to be easier than the second.
Another way functions may be tested is by naming a function with a variable instead of a strange symbol.
The function f is defined by f(x) = 3x(x+1). What is the value of f(5)?
This is the exact same question as the previous one, just formatted a little differently. You’re still going to replace each x with a 5.
f(5) = (3 × 5)(5 + 1)
f(5) = 15 × 6 = 90
PRACTICE DRILL 21—FUNCTIONS (MIDDLE AND UPPER LEVELS ONLY)
1.If  p = 5p — 4, then what is the value of
p = 5p — 4, then what is the value of  6 ?
6 ?
2.If f(x) = 7x, then what is the value of f(5)?
3.If p and q are positive integers and p  q is defined as
q is defined as 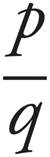 + 3, what is the value of 10
+ 3, what is the value of 10  2 ?
2 ?
4.The function s is defined by s(r) = r2 — 4. What is the value of s(3)?

When You Are Done
Check your answers in Chapter 3, this page.
MULTIPLYING EXPRESSIONS WITH FOIL (UPPER LEVEL ONLY)
First, Outside, Inside, Last
(x + 2)(x + 3)
FOIL stands for First, Outside, Inside, Last, an easy way to remember how to properly distribute all the terms of two binomials (expressions with two terms in them). Multiply the two First terms of each binomial, in this case x × x = x2. Then, multiply the Outside terms: x × 3 = 3x. Next, multiply the Inside terms: 2 × x = 2x. Finally, multiply the Last terms by each other: 2 × 3 = 6. Add all these terms together to find that (x + 2)(x + 3) = x2 + 3x +2x + 6. Combine like terms to fully simplify: x2 + 5x + 6.
Factoring with Binomials
To work in the opposite direction and factor a polynomial expression, create two sets of parentheses for the binomials and place a variable in each: (x )(x ). If the last term is positive, this means there must be either two plus signs or two minus signs. If both the middle and last terms are positive, there must be two plus signs, and if the middle term is negative when the last term is positive, there must be two minus signs. If the last term is negative, that means there must be one of each sign. Now, look at the last term. The two numbers in the parentheses must multiply to equal the last term and add to equal the middle term. Let’s try an example:
x2 + 6x + 9
Both terms are positive, so start with (x + )(x + ). Now, list the factors of 9: 1 and 9, 3 and 3. 1 + 9 ≠ 6, but 3 + 3 = 6. Therefore, the expression should read (x + 3)(x + 3). Let’s try another:
x2 — 3x — 10
This one has a negative sign before the last term, so start with (x + )(x — ) since a negative times a positive will equal a negative number. Now, list the factors of 10: 1 and 10, 2 and 5. Since the signs are opposite, there are more options of how to add the numbers, since 1 + —10 and —1 + 10 are both options. However, neither equals —3. Try 2 and 5: —2 + 5 = 3, and 2 + —5 = —3. Since the middle term must be negative, place the 2 with the plus sign and 5 with the minus sign: (x + 2)(x + —5).
PRACTICE DRILL 22—FOILING (UPPER LEVEL ONLY)
Factor the following expressions:
1.(x + 4)(x + 3)
2.(x — 4)(x — 3)
3.(x + 4)(x — 3)
4.(a + b)(a — b)
5.(a + b)(a + b)
6.(a — b)(a — b)
7.If x2 + y2 = 53, and xy = 14, what is the value of (x — y)2?
8.x2 + 13x + 42
9.y2 — 3y — 10
10.x2 — 12x + 35
11.y2 + 11x + 24
12.a2 — 5a — 14
13.b2 — 11b + 30
14.k2 + 16k + 63

When You Are Done
Check your answers in Chapter 3, this page.
Solving Percent Questions with Algebra—Middle and Upper Levels Only
Percentages
Solving percent problems can be easy when you know how to translate them from “percent language” into “math language.” Once you’ve done the translation, you guessed it—just manipulate the equation!
Whenever you see words from the following table, just translate them into math terms and go to work on the equation!

Learn a New Language
You can memorize “percent language” quickly because there are only four words you need to remember!
Percent Language |
Math Language |
% or “percent” |
out of 100 |
of |
times (as in multiplication) (×) |
what |
your favorite variable (p) |
is, are, were, was, did |
equals (=) |
For example:
“What percent” is represented by 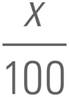 .
.
PRACTICE DRILL 23—TRANSLATING AND SOLVING PERCENT QUESTIONS (MIDDLE AND UPPER LEVELS ONLY)
1.30 is what percent of 250 ?
2.What is 12% of 200 ?
3.What is 25% of 10% of 200 ?
4.75% of 20% of what number is 12 ?
5.16% of what number is 25% of 80 ?
6.What percent is equal to ![]() ?
?
7.30 is what percent of 75 ?
8.What is 11% of 24 ?
9.What percent of 24 is equal to 48 ?
10.60% of what percent of 500 is equal to 6 ?

When You Are Done
Check your answers in Chapter 3, this page.
Averages
There are three parts to every average problem: total, number, and average. You may recall from the Math Vocabulary chart in Chapter 2 that the average is sometimes referred to as the mean. Most SSAT and ISEE problems will give you two of the three pieces and ask you to find the third. To help organize the information you are given, use the Average Pie.
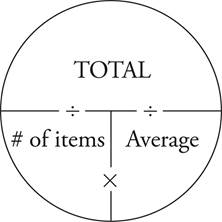
The Average Pie organizes all of your information visually. It makes it easier to see all of the relationships between pieces of the pie.
· TOTAL = (# of items) × (Average)
· # of items = 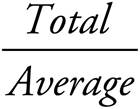
· Average = 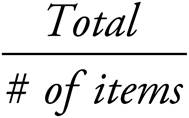
For example, if your friend went bowling and bowled three games, scoring 71, 90, and 100, here’s how you would compute her average score using the Average Pie.
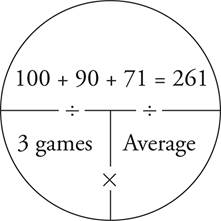
To find the average, you would simply write a fraction that represents 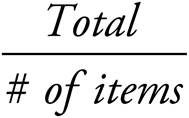 , in this case
, in this case 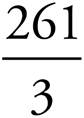 .
.
The math becomes simple. 261 ÷ 3 = 87. Your friend bowled an average of 87.
Get used to working with the Average Pie by using it to solve the following problems.
PRACTICE DRILL 24—AVERAGES (LOWER, MIDDLE, AND UPPER LEVELS ONLY)
1.The average of 3 numbers is 18. What is two times the sum of the 3 numbers?
2.An art club of 4 boys and 5 girls makes craft projects. If the boys average 2 projects each and the girls average 3 projects each, what is the total number of projects produced by the club?
3.Sofia scores 84, 85, and 88 on her first three exams. What must she score on her fourth exam to raise her average to an 89 ?
4.If a class of 6 students has an average grade of 72 before a seventh student joins the class, what must the seventh student’s grade be to raise the class average to 76 ?

When You Are Done
Check your answers in Chapter 3, this page.
More Practice (Lower Level)
5.Fatima ate 2 doughnuts on Monday, Wednesday, and Friday and ate 4 doughnuts on Tuesday and Thursday. She did not eat any doughnuts on Saturday or Sunday. What is the average number of doughnuts that Fatima ate each day of the week?
6.Merry drove 350 miles from New Orleans to Houston in 7 hours. She then drove 240 miles from Houston to Dallas in 4 hours. What was her approximate average rate of speed, in miles per hour (mph), for the entire trip?
7.A group of friends decided to compare comic book collections. Nathan has 11 comic books, Serena has 16, Jose has 14, and Amira has 19. What is the average number of comic books per person?
More Practice: Middle and Upper Levels
8.Michael scored an average of 24 points over his first 5 basketball games. How many points must he score in his 6th game to average 25 points over all 6 games?
9.Dwan measured a total of 245 inches of rainfall in his hometown over one week. During the same week the previous year, his hometown had a total of 196 inches. How many more inches was the average daily amount of rainfall for the week this year than the week last year?
10.Joe wants to find the mean number of pages in the books he has read this month. The books were 200, 220, and 260 pages long. He read the 200 page book twice, so it will be counted twice in the mean. If he reads one more book, what is the fewest number of pages it can have to make the mean no less than 230?

When You Are Done
Check your answers in Chapter 3, this page.
WORD PROBLEMS—ELEMENTARY, LOWER, MIDDLE, AND UPPER LEVELS ONLY
Many arithmetic and algebra problems are written in paragraph form with many words. The hard part is usually not the arithmetic or the algebra; the hard part is translating the words into math. So let’s focus on translating.
Key Words and Phrases to Translate
Specific words and phrases show up repeatedly in word problems. You should be familiar with all of those on this page.
What You Read in English |
What You Do in Math |
and, more than, the sum of, plus |
+ |
less than, the difference between, take away from |
— |
of, the product of, as much as |
× |
goes into, divided by, the quotient |
÷ |
is, are, was, were, the result will be, has, have, earns, equals, is the same as |
= |
what, what number, a certain number |
variable (x, y, z) |
half of a number |
|
twice as much as, twice as old as |
2x |
% (percent) |
|
how many times greater |
divide the two numbers |
Proportions—Lower, Middle, and Upper Levels Only
Proportions show relationships between two sets of information. For example, if you wanted to make cookies and you had a recipe for a dozen cookies but wanted to make two dozen cookies, you would have to double all of the ingredients. That’s a proportion. Here’s how we’d look at it in equation form.
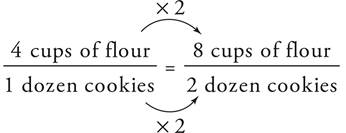
Whenever a question gives you one set of data and part of another set, it will ask you for the missing part of the second set of data. To find the missing information, set up the information in fractions like those on the previous page. Be careful to put the same information in the same place. In our example, we have flour on top and cookies on the bottom. Make sure both fractions have the flour over the cookies. Once we have our fractions set up, we can see what the relationship is between the two elements (in this case, flour and cookies). Whatever that relationship is, it’s the same as the relationship between the other two things.
PRACTICE DRILL 25—WORD PROBLEMS (LOWER, MIDDLE, AND UPPER LEVELS ONLY)
1.There are 32 ounces in 1 quart. 128 ounces equals how many quarts? How many ounces are there in 7 quarts?
2.A car travels at a rate of 50 miles per hour. How long will it take to travel 300 miles?
3.Betty is twice as old as her daughter Fiona. Fiona is twice as old as her dog Rufus. If Rufus is 11, how old is Betty?
4.A clothing store sold 1,250 pairs of socks this year. Last year, the store sold 250 pairs of socks. This year’s sales are how many times greater than last year’s sales?
5.There are 500 students at Eisenhower High School. ![]() of the total students are freshmen.
of the total students are freshmen. ![]() of all the freshmen are girls. How many freshman girls are there?
of all the freshmen are girls. How many freshman girls are there?

When You Are Done
Check your answers in Chapter 3, this page.
GEOMETRY—PRIMARY 4, ELEMENTARY, LOWER, MIDDLE, AND UPPER LEVELS ONLY
An Introduction
Just as in the previous Algebra section, this Geometry section contains some material that is above the level tested on the Lower/Elementary and Middle Level Exams. These students should not work on sections that are indicated for higher levels.
Perimeter—Primary 4, Elementary, Lower, Middle, and Upper Levels Only
The perimeter is the distance around the outside of any figure. To find the perimeter of a figure, just add up the lengths of all the sides.
Perimeter
P = side + side + side...until you run out of sides.
What are the perimeters of these figures?
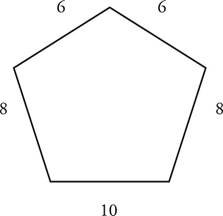
Perimeter = 6 + 6 + 8 + 8 + 10 = 38
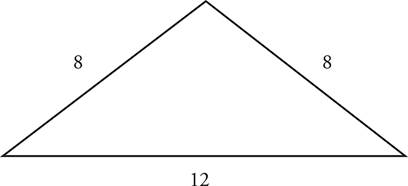
Perimeter = 8 + 8 + 12 = 28
Angles—Middle and Upper Levels Only
Straight Lines
Angles that form a straight line always total 180°.
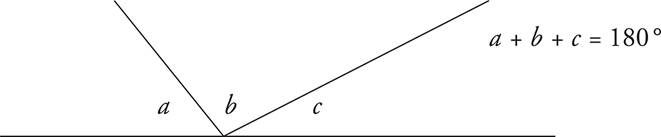
The Rule of 180°
There are 180° in a straight line and in a triangle.
Triangles
All of the angles in a triangle add up to 180°.
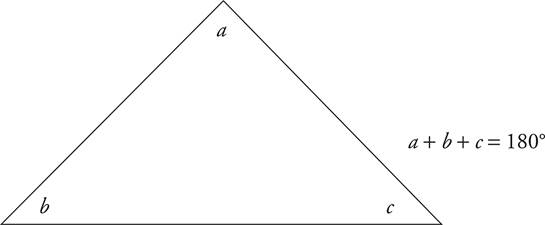
Four-Sided Figures
The angles in a square, rectangle, or any other four-sided figure always add up to 360°.
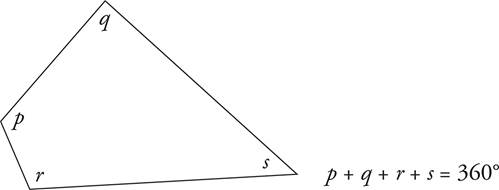
The Rule of 360°
There are 360° in a four-sided figure and in a circle.
Angle Vocabulary
Supplementary Angles are angles that add up to 180°.
Complementary Angles are angles that add up to 360°.
Opposite Angles are the angles that are across from one another when two lines cross. They are always equal!
Vertex is the point at which two lines (or sides of a polygon) cross or meet.
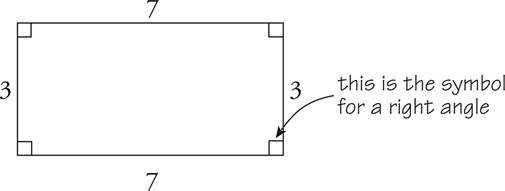
Squares and Rectangles—Elementary, Lower, Middle, and Upper Levels Only
A rectangle is a four-sided figure with four right (90°) angles. Opposite sides are equal in a rectangle. The perimeter is equal to the sum of the sides.
Perimeter = 3 + 3 + 7 + 7 = 20
A square is a special type of rectangle in which all the sides are equal.
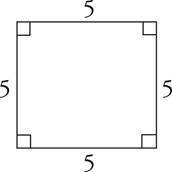
Perimeter = 5 + 5 + 5 + 5 = 20
Because all sides of a square are equal, you can find the length of a side by dividing its perimeter by four. If the perimeter of a square is 20, then each side is 5, because 20 ÷ 4 = 5.
Area—Elementary, Lower, Middle, and Upper Levels Only
Area is the amount of space taken up by a two-dimensional figure. One way to think about area is as the amount of paper that a figure covers. The larger the area, the more paper the figure takes up.
To determine the area of a square or rectangle, multiply the length (l) by the width (w).
Remember the formula:
Area = length × width
What is the area of a rectangle with length 9 and width 4 ?
In this case, the length is 9 and the width is 4, so 9 × 4 = 36. Now look at another example.
Area of a Rectangle
A = lw

The area of squares and rectangles is given in square feet, square inches, and so on.
To find the area of a square, you multiply two sides, and because the sides are equal, you’re really finding the square of the sides. You can find the length of a side of a square by taking the square root of the area. So if a square has an area of 25, one side of the square is 5.
Area of a Square
A = s2
Volume—Lower, Middle, Upper Levels Only
Volume is very similar to area, except it takes into account a third dimension. To compute the volume of a figure, you simply find the area and multiply by a third dimension.
For instance, to find the volume of a rectangular object, you would multiply the length by the width (a.k.a. the area of the base) by the height (the third dimension). Since a rectangular solid (like a box) is the only kind of figure you are likely to see in a volume question, simply use the formula below.
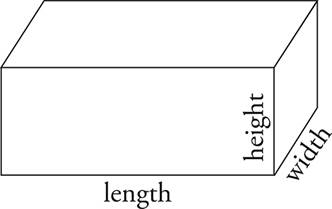
length × width × height = volume
Volume of a Rectangular Solid
V = lwh
For example:
What is the volume of a rectangular fish tank with the
following specifications?
length: 6 inches
height: 6 inches
width: 10 inches
There isn’t much to it. Just plug the numbers into the formula.
length × width × height = volume
6 × 10 × 6 = 360
PRACTICE DRILL 26—SQUARES, RECTANGLES, AND ANGLES—LOWER, MIDDLE, AND UPPER LEVELS ONLY
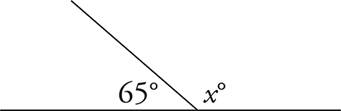
1.What is the value of x ?
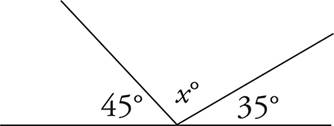
2.What is the value of x ?
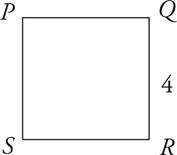
3.PQRS is a square. What is its perimeter? Area?

4.ABCD is a rectangle with length 7 and width 3. What is its perimeter? Area?
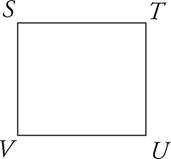
5.STUV is a square. Its perimeter is 12. What is its area?
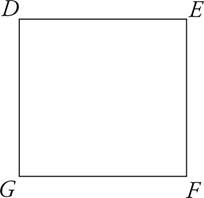
6.DEFG is a square. Its area is 81. What is its perimeter?

7.JKLM is a rectangle. If its width is 4, and its perimeter is 20, what is its area?

8.WXYZ is a rectangle. If its length is 6 and its area is 30, what is its perimeter?
9.What is the volume of a rectangular solid with height 3, width 4, and length 2 ?

When You Are Done
Check your answers in Chapter 3, this page.
Triangles—Elementary, Lower, Middle, Upper Levels Only
A triangle is a geometric figure with three sides.
Isosceles Triangles
Any triangle with two equal sides is an isosceles triangle.
If two sides of a triangle are equal, the angles opposite those sides are always equal. Said another way, the sides opposite the equal angles are also equal.
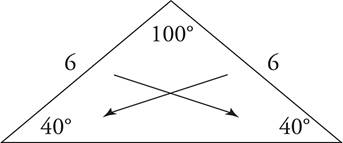
This particular isosceles triangle has two equal sides (of length 6) and therefore two equal angles (40° in this case).
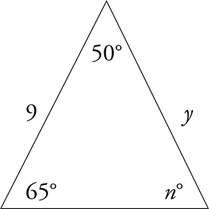
If you already know that the above triangle is isosceles, then you also know that y must equal one of the other sides and n must equal one of the other angles. Since n = 65 (65° + 50° + n° = 180°), then y must equal 9, because it is opposite the other 65° angle.
Equilateral Triangles
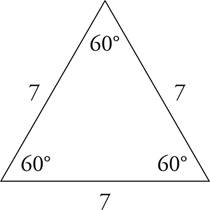
An equilateral triangle is a triangle with three equal sides. If all the sides are equal, then all the angles must be equal. Each angle in an equilateral triangle is 60°.
Right Triangles
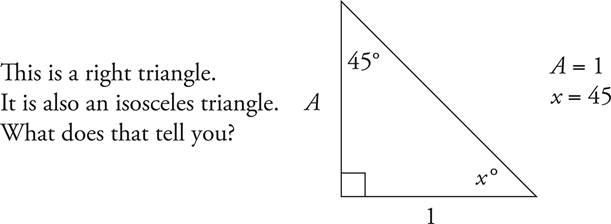
A right triangle is a triangle with one 90° angle.

Area
To find the area of a triangle, multiply ![]() by the length of the base by the length of the triangle’s height, or
by the length of the base by the length of the triangle’s height, or 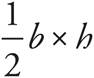 .
.
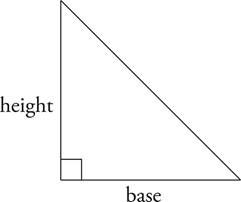
What is the area of a triangle with base 6 and height 3 ?
(A) 3
(B) 6
(C) 9
(D) 12
(E) 18

Elementary and Lower Levels
The test-writers may give you the formula for the area of a triangle, but memorizing it will still save you time!
Just put the values you are given into the formula and do the math. That’s all there is to it!
![]() b × h = area
b × h = area
(![]() )(6) × 3 = area
)(6) × 3 = area
× 3 = 9
So, (C) is the correct answer.
Don’t Forget!
A = ![]() bh
bh
Remember the base and the height must form a 90°-angle.
The only tricky point you may run into when finding the area of a triangle is when the triangle is not a right triangle. In this case, it becomes slightly more difficult to find the height, which is easiest to think of as the distance to the point of the triangle from the base. Here’s an illustration to help.
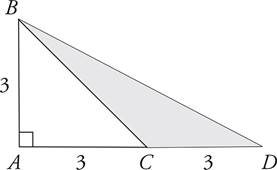
First look at triangle BAC, the unshaded right triangle on the left side. Finding its base and height is simple—they are both 3. So using our formula for the area of a triangle, we can figure out that the area of triangle BAC is 4![]() .
.
Now let’s think about triangle BCD, the shaded triangle on the right. It isn’t a right triangle, so finding the height will involve a little more thought. Remember the question, though: how far up from the base is the point of triangle BCD? Think of the shaded triangle sitting on the floor of your room. How far up would its point stick up from the floor? Yes, 3! The height of triangle BCD is exactly the same as the height of triangle BAC. Don’t worry about drawing lines inside the shaded triangle or anything like that, just figure out how high its point is from the ground.
Okay, so just to finish up, to find the area of triangle BCD (the shaded one), use the same area formula, and just plug in 3 for the base and 3 for the height.
![]() b × h = area
b × h = area
(![]() )(3) × 3 = area
)(3) × 3 = area
And once you do the math, you’ll see that the area of triangle BCD is 4![]() .
.
Not quite convinced? Let’s look at the question a little differently. The base of the entire figure (triangle DAB) is 6, and the height is 3. Using your trusty area formula, you can determine that the area of triangle DAB is 9. You know the area of the unshaded triangle is 4![]() , so what’s left for the shaded part? You guessed it, 4
, so what’s left for the shaded part? You guessed it, 4![]() .
.
Similar Triangles—Middle and Upper Levels Only
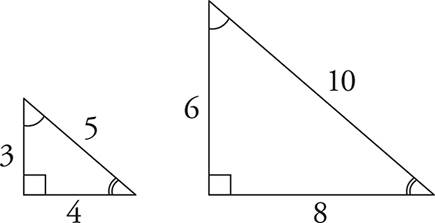
Similar triangles are triangles that have the same angles but sides of different lengths. The ratio of any two corresponding sides will be the same as the ratio of any other two corresponding sides. For example, a triangle with sides 3, 4, and 5 is similar to a triangle with sides of 6, 8, and 10, because the ratio of each of the corresponding sides (3:6, 4:8, and 5:10) can be reduced to 1:2.
One way to approach similar triangles questions that ask you for a missing side is to set up a ratio or proportion. For example, look at the question below:
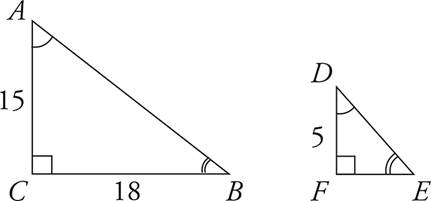
What is the value of EF?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8
These triangles are similar because they have the same angles. To find side EF, you just need to set up a ratio or proportion.
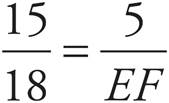
Cross-multiply to get 15(EF) = 18(5).
Divide both sides by 15 to get EF = 6.
Therefore, the answer is (C), 6.
The Pythagorean Theorem—Upper Level Only
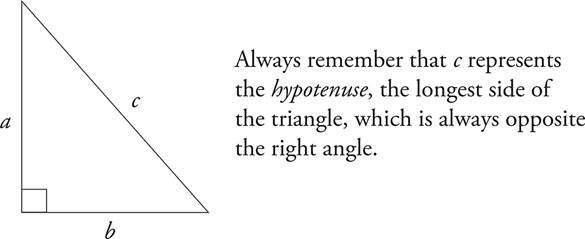
For all right triangles, a2 + b2 = c2, where a, b, and c are the lengths of the triangle’s sides.
Try It!
Test your knowledge of triangles with the problems that follow. If the question describes a figure that isn’t shown, make sure you draw the figure yourself!
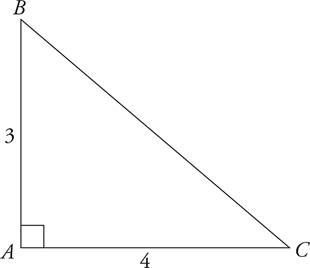
1.What is the length of side BC ?
(A) 4
(B) 5
(C) 6
(D) 7
(E) 8
Just put the values you are given into the formula and do the math, remembering that line BC is the hypotenuse:
a2 + b2 = c2
32 + 42 = c2
9 + 16 = c2
25 = c2
5 = c
So, (B) is the correct answer.
PRACTICE DRILL 27—TRIANGLES (ELEMENTARY, LOWER, MIDDLE, AND UPPER LEVELS ONLY)
1.What is the value of x ?
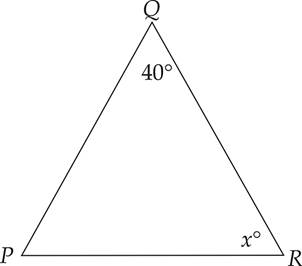
2.Triangle PQR is an isosceles triangle. PQ = QR. What is the value of x ?
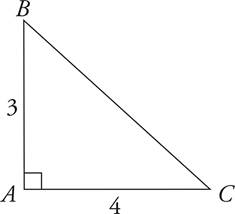
3.What is the area of right triangle ABC ?
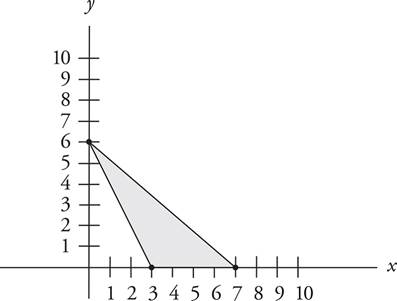
4.What is the area of the shaded region?
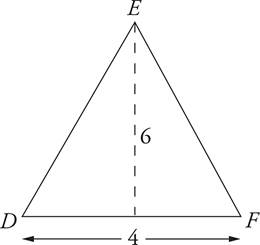
5.What is the area of triangle DEF ?

6.What is the area of triangle WXZ ? Triangle ZXY ? Triangle WXY ?
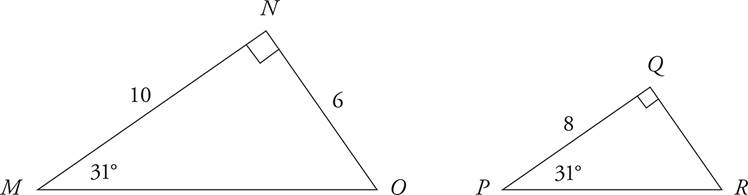
7.What is the length of line QR ?
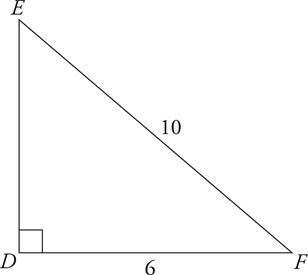
8.What is the length of side DE ?
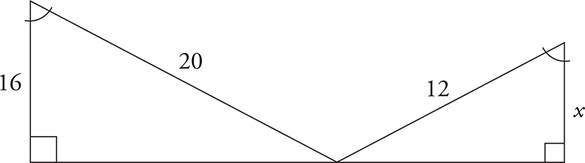
9.What is the value of x ?
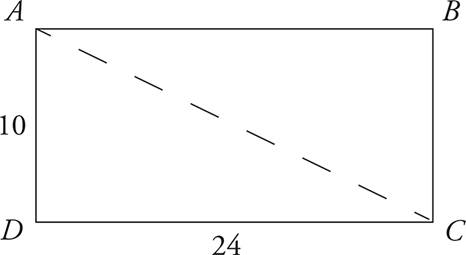
10.What is the length of the diagonal of rectangle ABCD ?
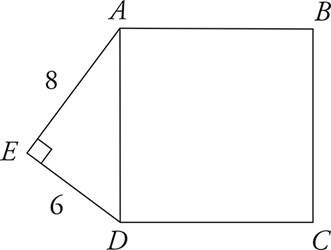
11.What is the perimeter of square ABCD ?
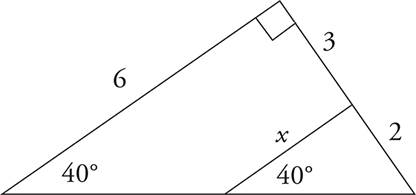
12.What is the value of x ?

When You Are Done
Check your answers in Chapter 3, this page.
Circles—Middle and Upper Levels Only
You are probably already familiar with the parts of a circle, but let’s review them anyway.
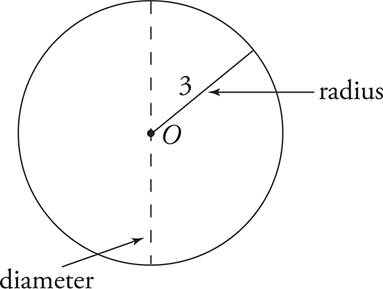
Any line drawn from the origin (the center of the circle) to its edge is called a radius (r).
Any line that goes from one side of the circle to the other side and passes through the center of the circle is called the diameter (d). The diameter is two times the length of the radius.
Diameter
d = 2r
Circumference
C = πd
Area
A = πr2
Area and Circumference
Circumference (which is written as C) is really just the perimeter of a circle. To find the circumference of a circle, use the formula 2πr or πd. We can find the circumference of the circle above by taking its radius, 3, and multiplying it by 2π.
C = 2πr
C = 2π3
C = 6π
The area of a circle is found by using the formula πr2.
A = πr2
A = π32
A = 9π
You can find a circle’s radius from its circumference by getting rid of π and dividing the number by 2. Or you can find the radius from a circle’s area by getting rid of π and taking the square root of the number.
So if a circle has an area of 81π, its radius is 9. If a circle has a circumference of 16π, its radius is 8.
What’s up with π?
The Greek letter π is spelled “pi” and pronounced “pie.” It is a symbol used with circles. Written as a number, π is a nonrepeating, nonending decimal (3.1415927…). We use π to determine the true length of circles. However, on the ISEE and SSAT, we simply leave π as the Greek letter. So when figuring out area or circumference, make sure that you include π in your equation at the beginning and include it in every step of your work as you solve. Remember, π represents a number and it must always be included in either the area or circumference formula.
PRACTICE DRILL 28—CIRCLES (MIDDLE AND UPPER LEVELS ONLY)
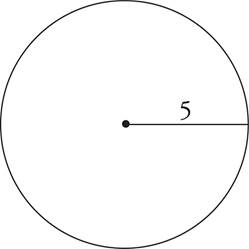
1.What is the circumference of the above circle? What is the area?
2.What is the area of a circle with radius 4 ?
3.What is the area of a circle with diameter 8 ?
4.What is the radius of a circle with area 9π ?
5.What is the diameter of a circle with area 9π ?
6.What is the circumference of a circle with area 25π ?

When You Are Done
Check your answers in Chapter 3, this page.
3-D Shapes—Upper Level Only
Both the SSAT and ISEE Upper Level tests include 3-D shape geometry questions. While these question types tend to be few and far between, it is important you are prepared for them, just in case they do come up.
Boxes
A three-dimensional box has three important lines: length, width, and height.
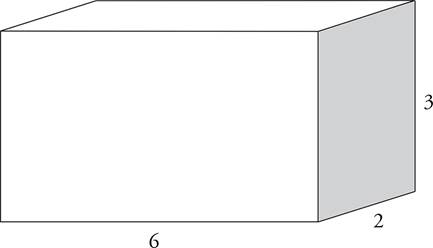
This rectangular box has a length of 6, a width of 2, and a height of 3.
The volume formula of a rectangular box is V = lwh.
V = lwh
V = 6(2)(3)
V = 36
Cubes
Cubes are just like rectangular boxes, except that all the sides are equal.
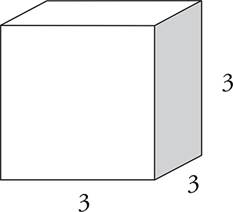
The volume formula for the cube is still just V = lwh, but since the length, width, and height are all equal it can also be written as V = s3, where s = side.
V = s3
V = 33
V = 27
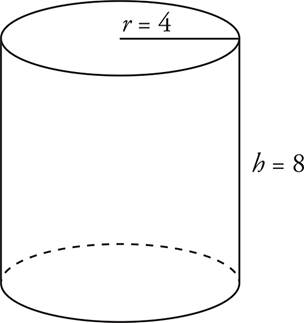
Cylinders
Cylinders are like circles with height added. For a cylinder with a radius of r and a height of h, the volume formula is V = πr2h.
V = πr2h
V = π224
V = π4(4)
V = 16π
PRACTICE DRILL 29—3-D SHAPES (UPPER LEVEL ONLY)
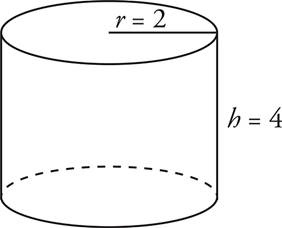
1.What is the volume of this cylinder?
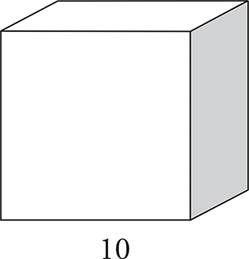
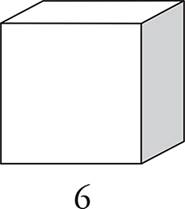
2.What is the volume of this cube?
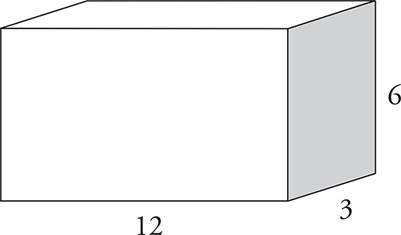
3.What is the volume of this rectangular box?
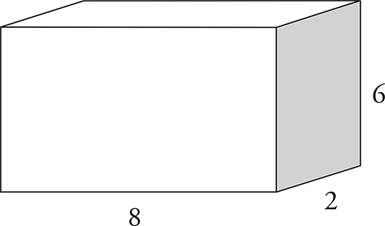
4.A cube with a side length of 6 inches has 54 cubic inches poured into it. How many more cubic inches must be poured into the cube for it to be completely filled?
5.The rectangular box pictured is filled by identical cubes with side lengths of 2. How many cubes does it take to fill the rectangular box?

6.The cylinder pictured is ![]() full of grain. What is the volume of the grain in the cylinder?
full of grain. What is the volume of the grain in the cylinder?

When You Are Done
Check your answers in Chapter 3, this page.
COORDINATE GEOMETRY—LOWER, MIDDLE, AND UPPER LEVELS ONLY
The xy-Coordinate Plane
Coordinate geometry tests the same material as plane geometry, just on an xy-coordinate plane. Think of the xy-coordinate plane as a map of sorts: the x-axis runs left to right, similar to how east and west work on a map, and the y-axis runs up and down, or north and south. Both axes work like number lines in positive and negative directions, stretching infinitely in both directions. Ordered pairs (x, y) indicate where on the map to plot points, the first number always referring to the x-axis and the second always referring to the y-axis. The x- and y-axes cross one another at the origin, point (0, 0), and all other points are in reference to the origin. Everything to the right of the origin has a positive x-value while everything to the left has a negative x-value. Points above the x-axis have a positive y-value, while points below the x-axis have a negative y-value. Think of this concept as the equator splitting the earth in two.
Look at the following figure, for example. The point (4, 5) indicates to travel from the origin four in the positive direction on the x-axis, and then five in the positive direction on the y-axis. Similarly, point (—4, 5) travels in the negative direction on the x-axis, but in the positive direction on the y-axis.
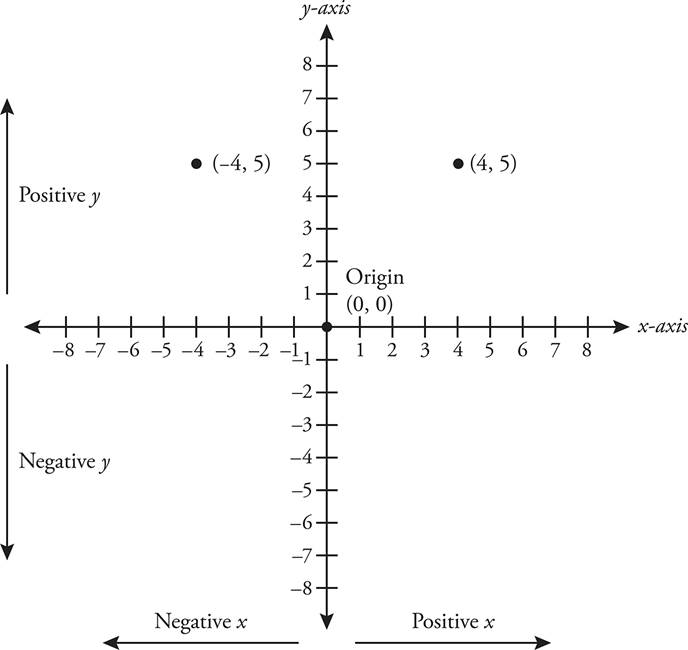
Try some on your own! Plot the following points: (1, 7), (—1, 7), (1, —7)
What kind of shape do these points create if you connect them? If you answered triangle, you are correct. Connecting points to create shapes can very easily turn a coordinate geometry question into a plane geometry question.
Formula of a Line
Coordinate planes are also useful for plotting lines, shapes, and curves. For these tests, it is especially useful to understand how the formula of a line works. The most common form of the line formula is called slope-intercept form because it shows the slope and the y-intercept:
y = mx + b
The x and y in the formula represent the two parts of an ordered pair. m represents the slope and shows how steep or shallow the line’s incline or decline is. A positive slope means that the line will rise from left to right and a negative slope will descend from left to right. To find m, you will need two points along the line to find the rise over run. Any two points define a line by connecting them together, so it does not matter which you use. The “rise” refers to the change in the y-axis, and the “run” to the change in the x-axis. Use the following formula to calculate the slope and be sure to remain consistent as to which point you call the first point and which you call the second so the order matches in the numerator and denominator.
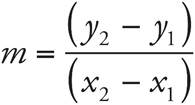
Let’s try an example:
![]()
Points (2, 6) and (—1, 0) lie on a certain line. What is its slope?
(A) —4
(B) —2
(C) 2
(D) 4
Here’s How to Crack It
Use the slope formula using the (x, y) ordered pairs. Let’s call (2, 6) the first point, (x1, y1), and (—1, 0) the second, or (x2, y2). Therefore, the slope equation will read 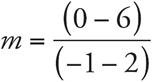 . Simplify the numerator and the denominator to find that
. Simplify the numerator and the denominator to find that 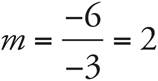 . This slope will be an upward slope. The correct answer is (C).
. This slope will be an upward slope. The correct answer is (C).
![]()
The other important component to slope intercept form is the y-intercept, the y-value when x is zero. You can find this point if you know the slope and any point. In the previous example, the slope is 2, and you already know two points. The formula should read y = 2x + b, so to solve for b, choose a point to plug in for x and y. Try using (2, 6), for example. The equation will become 6 = 2(2) + b. Multiply 2 by 2 to find that 6 = 4 + b. Then, subtract 4 from both sides to isolate b. Since b = 2, the point (0, 2) must also be a point on the same line. The final equation to the line containing all these points is y = 2x + 2.
Parallel and Perpendicular Lines—Middle and Upper Levels Only
Lines parallel to each other will have the same slope and different y-intercepts, meaning that they will travel in the same direction and never intersect. Lines that are perpendicular to one another intersect at a 90º angle. Therefore, their slopes will be the negative reciprocals of one another. For example, if the slope of one of the lines is 2, the slope of the line perpendicular would be 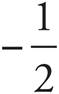 . If the slope were
. If the slope were ![]() , the slope of the line perpendicular would be
, the slope of the line perpendicular would be 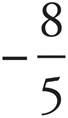 . Try a sample question.
. Try a sample question.
![]()
The line y= 3x + 2 contains no solutions with which of the following lines?
(A) y = 3x + 2
(B) y = —3x — 2
(C) 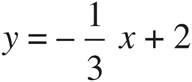
(D) y = 3x + 3
Here’s How to Crack It
The test-makers sometimes use fancy language, but a “solution” is the same as an intersection. If the lines never intersect, that must mean they are parallel to one another, and therefore have the same slope. Eliminate (B) and (C). For the lines to be parallel, they cannot be the same line, which would have the same y-intercept. Therefore, eliminate (A) and the correct answer is (D).
![]()
PRACTICE DRILL 30—COORDINATE GEOMETRY (MIDDLE AND UPPER LEVELS ONLY)
1.What is the slope of a line perpendicular to 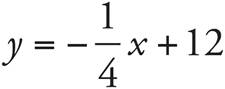 ?
?
2.What is the equation of the line shown above?
3.What could be the fourth coordinate of a parallelogram with the points (3, —4), (3, 8), and (—4, —4)?
4.What is the slope of the line containing points (—2, 12) and (3, 5)?
5.
Which value would be greater?
a) the slope of a line that is parallel to line k
b) the slope of a line that is perpendicular to line k

When You Are Done
Check your answers in Chapter 3, this page.
TRIGONOMETRY—UPPER LEVEL ISEE ONLY
Trigonometry is a helpful way of using angle measurements and side relationships to find missing information about triangles of all types. On the ISEE, test makers will generally stick to right triangles, either isolated or in real-world applications. These measurements can be used for more complicated shapes, though these will not appear on this test.
SOHCAHTOA
SOHCAH…what? SOHCAHTOA is a helpful mnemonic device to help you remember the basic relationships of trigonometry. S stands for sine, C for cosine, and T for tangent for an angle, θ. Each of these represents ratios between the sides and hypotenuse of a right triangle. O, A, and H stand for opposite, adjacent, and hypotenuse sides of the triangle. The hypotenuse is always the longest side of a right triangle, opposite the right angle. The opposite and adjacent sides are the legs of a right triangle. The mnemonic spells out the following expressions:
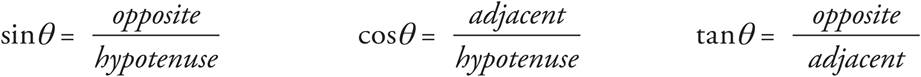
SOH stands for 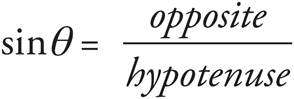 , CAH stands for
, CAH stands for 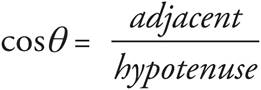 , and TOA stands for
, and TOA stands for 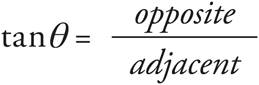 .
.
Which side is adjacent and which is opposite? It all depends on which angle you are relating the sides to. Take a look at the following triangle:

In the figure above, YZ is the hypotenuse because it is opposite the right angle. Angle Z is opposite side XY and adjacent to side XZ (since it’s touching the angle). Likewise, Angle Y is opposite side XZ and adjacent to XY.
Let’s try an example.
![]()
What is the length of side BC?
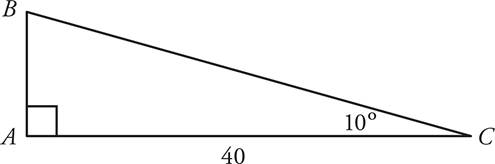
(A) 40sin 10°
(B) 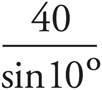
(C) 40cos 10°
(D) 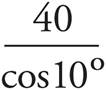
Here’s How to Crack It
Identify BC. In this case, it is the hypotenuse of the triangle. The other pieces of information will determine which measurement to use of SOHCAHTOA. Since side AC and angle C are given, it seems most convenient to use cosine, as AC is adjacent to angle C. Eliminate (A) and (B), since those contain sine measurements. Cosine is the CAH of SOHCAHTOA, which stands for Cosine = Adjacent/Hypotenuse. Therefore, 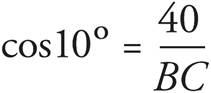 . Multiply both sides of the equation by BC to find that BC cos10°= 40. Finally, divide both sides by cos 10° to find that
. Multiply both sides of the equation by BC to find that BC cos10°= 40. Finally, divide both sides by cos 10° to find that 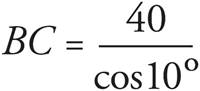 . The correct answer is (D).
. The correct answer is (D).
![]()
PRACTICE DRILL 31—TRIGONOMETRY (UPPER LEVEL ISEE ONLY)
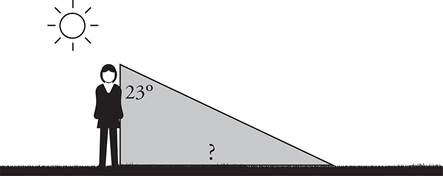
1.Samin is standing in an open field on a sunny day. The sun hits her at a 23º angle. If Samin is 1.5 meters tall, how long is her shadow on the ground?
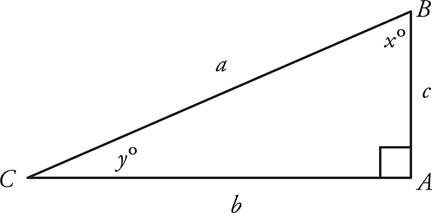
2.What is cos x?

3.A 50-foot ramp contains a 5º incline. How high is h shown above?
4.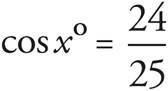 . What is sin yº?
. What is sin yº?
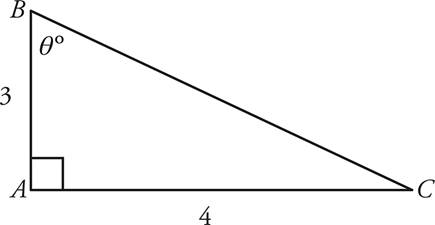
5.Triangle ABC contains sides with lengths 3 and 4 as shown above. What is sin θ?

When You Are Done
Check your answers in Chapter 3, this page.
PROBABILITY—LOWER, MIDDLE, AND UPPER LEVELS ONLY
Probability describes how likely it is that something is going to happen. You might not have quantified it before, but it’s something you do every day, whether you’re flipping a coin or wondering if you’ll need to take an umbrella. To make probability less vague, many people express the odds of something happening in terms of percents. For instance, a standard coin has two equal results: heads (50%) and tails (50%). If the weather report says that there’s a 90% chance of rain, you probably want to take that umbrella. You might also see probability expressed as a number between 0 and 1—the chance of seeing a flying elephant being 0 and the chance of the sun rising tomorrow being 1.
Don’t be distracted by the objects in the question or the method with which they’re being assessed. Whether it’s 20% or 0.2, whether dealing with marbles, cards, coins, food, or anything else, a probability question essentially boils down to finding a specific number of possibilities out of the total number of possibilities.

Percents Make Per-sense
Remember that the word percent translates to  . Therefore, a probability of 0% is the same as a probability
. Therefore, a probability of 0% is the same as a probability 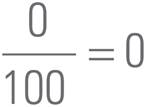 , and a probability of 100% is the same as a probability of
, and a probability of 100% is the same as a probability of 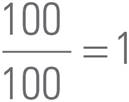 . Any probability between 0% and 100% is equivalent to a probability between 0 and 1.
. Any probability between 0% and 100% is equivalent to a probability between 0 and 1.
Independent Probability
The basic formula for probability is
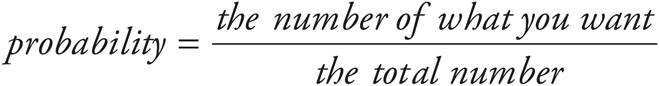
For example, if a bag with 11 total gumballs has 6 red gumballs, the probability of randomly selecting a red gumball is 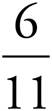 , or 0.54, or 54%.
, or 0.54, or 54%.
![]()
A gumball is randomly selected from a jar that contains 5 blue gumballs, 15 red gumballs, and 30 yellow gumballs. What is the probability that the randomly selected gumball is red?
(A) 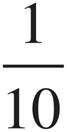
(B) 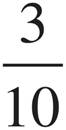
(C) ![]()
(D) ![]()
Here’s How to Crack It
The question asks for probability, so use the formula probability 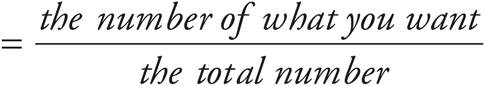 . The question asks for the probability that a randomly selected gumball is red, so the number you want is the number of red gumballs, which is 15, and the total number is the number of gumballs, which is 5 + 15 + 30 = 50. Therefore, the probability is
. The question asks for the probability that a randomly selected gumball is red, so the number you want is the number of red gumballs, which is 15, and the total number is the number of gumballs, which is 5 + 15 + 30 = 50. Therefore, the probability is 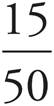 . This is not a choice, so reduce the fraction. Both the numerator and denominator are multiples of 5, so divide both by 5 to get
. This is not a choice, so reduce the fraction. Both the numerator and denominator are multiples of 5, so divide both by 5 to get ![]() , which is (B).
, which is (B).
![]()
“Not” Probability—Middle and Upper Levels Only
So-called “not” probability is just the probability that something will not happen. To find this, determine the probability that the event will happen and subtract that number from 1. It’s often easier than calculating the probability of all other possible outcomes and adding all of those together to get the answer. Remember, the bag with 11 total gumballs has 6 red gumballs. The probability of randomly selecting a red gumball is 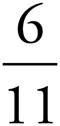 , so the probability of not selecting a red gumball is
, so the probability of not selecting a red gumball is 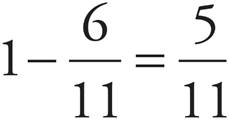 .
.
“Or” Probability—Middle and Upper Levels Only
Sometimes the question will ask for the probability of one event or another event taking place. To find this, add the individual probabilities. For example, take that same bag with 11 gumballs, 6 of which are red. Of the remaining 5, 3 are blue gumballs and 2 are yellow gumballs. The probability of getting a red gumball or a blue gumball is 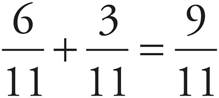 . The probability of getting a blue gumball or a yellow gumball is
. The probability of getting a blue gumball or a yellow gumball is 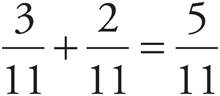 . Notice that this is the same as the probability of not getting a red gumball. The probability of getting a red gumball, a blue gumball, or a yellow gumball is
. Notice that this is the same as the probability of not getting a red gumball. The probability of getting a red gumball, a blue gumball, or a yellow gumball is 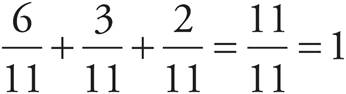 . The probability is 1, because red, blue, and yellow are the only colors of gumballs in the bag, so one of these colors must be drawn.
. The probability is 1, because red, blue, and yellow are the only colors of gumballs in the bag, so one of these colors must be drawn.
![]()
|
COLORS OF THE RAINBOW SURVEY |
|
Color |
Number of Students |
Red |
13 |
Orange |
15 |
Yellow |
17 |
Green |
31 |
Blue |
24 |
Indigo |
6 |
Violet |
29 |
The students at a school were surveyed and asked for their favorite color of the rainbow. What is the probability that a randomly selected student chose either red or yellow as her favorite color?
(A) 
(B) 
(C) ![]()
(D) ![]()
Here’s How to Crack It
The question asks for the probability that a randomly selected student chooses either red or yellow, so add the probability that the student selects red to the probability that the student selects yellow. To find each of these, determine the total number of students in the poll. The total number is 13 + 15 + 17 + 31 + 24 + 6 + 29 = 135. There are 13 students who select red, so the probability of selecting red is 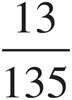 . There are 17 students who select yellow, so the probability of selecting yellow is
. There are 17 students who select yellow, so the probability of selecting yellow is 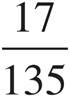 . Therefore, the probability of selecting red or yellow is
. Therefore, the probability of selecting red or yellow is 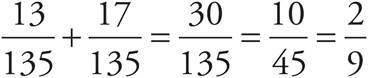 which is (C).
which is (C).
![]()
“And” Probability—Middle and Upper Levels Only
On SSAT and ISEE probability questions, it is important to decide if there are any events that happen independently from each other, or if one event affects another. For instance, if a question asks about flipping a coin four times, does one coin flip influence the next? The answer is no. A coin flip will come out to either heads or tails every time, so the probability of getting tails on each trial is ![]() . However, in some cases, one event does affect the next, which is when you’ll want to know about “and” probability. This concept still uses basic probability. Take the probability that each individual event happens and multiply them.
. However, in some cases, one event does affect the next, which is when you’ll want to know about “and” probability. This concept still uses basic probability. Take the probability that each individual event happens and multiply them.
Once again, consider the bag with 11 gumballs, including 6 red gumballs. If two gumballs are selected at random, what is the probability that they will both be red? The probability that the first gumball will be red is 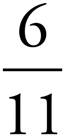 . However, the probability that the second gumball will be red is different. Once one red gumball is removed, only 5 red gumballs and 10 total gumballs remain, so the probability is
. However, the probability that the second gumball will be red is different. Once one red gumball is removed, only 5 red gumballs and 10 total gumballs remain, so the probability is 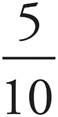 . To find the probability that both are red, multiply the two individual probabilities to get
. To find the probability that both are red, multiply the two individual probabilities to get 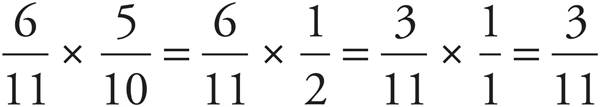 .
.
![]()
Josh has 3 T-shirts, 4 long-sleeved shirts, and 7 tank tops. If he selects two shirts at random, what is the probability that both shirts will be tank tops?
(A) 
(B) ![]()
(C) 
(D) ![]()
Here’s How to Crack It
To find the probability that both shirts will be tank tops, find the probability that each individual shirt will be a tank top. There are 7 tank tops and 3 + 4 + 7 = 14 total shirts, so the probability that the first shirt will be a tank top is 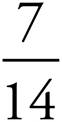 . Once one tank top is removed, there are 6 tank tops and 13 total shirts remaining, so the probability that the second shirt will be a tank top is
. Once one tank top is removed, there are 6 tank tops and 13 total shirts remaining, so the probability that the second shirt will be a tank top is 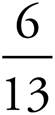 . Therefore, the probability that both will be tank tops is
. Therefore, the probability that both will be tank tops is 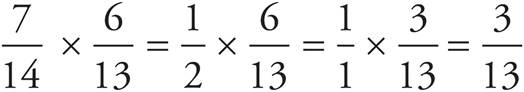 , which is (A).
, which is (A).
![]()
PRACTICE DRILL 32—PROBABILITY
Lower, Middle, Upper
1.A basket of marbles contains 15 blue marbles. If the probability of not selecting a blue marble is ![]() , how many marbles are in the basket?
, how many marbles are in the basket?
2.A bowl of fruit contains 4 apples, 6 kiwis, and 5 oranges. If one fruit is selected from the bowl at random, what is the probability that it will be an apple or a kiwi?
Middle and Upper only
3.A box of cookies has 2 chocolate chip, 4 pecan, 7 oatmeal raisin, and 3 peanut butter cookies. If two cookies are selected at random, what is the probability that both cookies will be pecan?
4.A jar of cookies contains 5 chocolate chip, 4 oatmeal raisin, 4 snicker doodles, and 2 red velvet. Sandy chooses two cookies from the jar without replacement. What is the probability that she will choose a chocolate chip cookie first and a red velvet cookie second?

When You Are Done
Check your answers in Chapter 3, this page.
CHARTS AND GRAPHS—ALL LEVELS
Charts
Chart questions usually do not involve much computation, but you must be careful. Follow these three steps and you’ll be well on the way to mastering any chart question.
1.Read any text that accompanies the chart. It is important to know what the chart is showing and what scale the numbers are on.
2.Read the question.
3.Refer to the chart and find the specific information you need.
If there is more than one question about a single chart, the later questions will tend to be more difficult than the earlier ones. Be careful!

Don’t Be in Too Big a Hurry
When working with charts and graphs, make sure you take a moment to look at the chart or graph, figure out what it tells you, and then go to the questions.
Here is a sample chart.
Club Membership by State, 2021 and 2022
State |
2021 |
2022 |
California |
300 |
500 |
Florida |
225 |
250 |
Illinois |
200 |
180 |
Massachusetts |
150 |
300 |
Michigan |
150 |
200 |
New Jersey |
200 |
250 |
New York |
400 |
600 |
Texas |
50 |
100 |
There are many different questions that you can answer based on the information in this chart. For instance:
What is the difference between the number of members who came from New York in 2021 and the number of members who came from Illinois in 2022?
This question asks you to look up two simple pieces of information and then do a tiny bit of math.
First, the number of members who came from New York in 2021 was 400.
Second, the number of members who came from Illinois in 2022 was 180.
Finally, look back at the question. It asks you to find the difference between these numbers. 400 — 180 = 220. Done.
The increase in the number of members from New Jersey from 2021 to 2022 was what percent of the total number of members in New Jersey in 2021 ?
You should definitely know how to do this one! Do you remember how to translate percentage questions? If not, go back to the percentage discussion earlier in the chapter.
In 2021, there were 200 club members from New Jersey. In 2022, there were 250 members from New Jersey. That represents an increase of 50 members. To determine what percent that is of the total amount in 2021, you need to ask yourself, “50 (the increase) is what percent of 200 (the number of members in 2021)?”
Translated, this becomes:
50 = 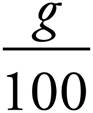 × 200
× 200
With a little bit of simple manipulation, this equation becomes:
50 = 2g
and
25 = g
So from 2021 to 2022, there was a 25% increase in the number of members from New Jersey. Good work!
Which state had as many club members in 2022 as a combination of Illinois, Massachusetts, and Michigan had in 2021 ?
First, take a second to look up the number of members who came from Illinois, Massachusetts, and Michigan in 2021 and add them together.
200 + 150 + 150 = 500
Which state had 500 members in 2022? California. That’s all there is to it!
Graphs
Some questions will ask you to interpret a graph. You should be familiar with both pie and bar graphs. These graphs are generally drawn to scale (meaning that the graphs give an accurate visual impression of the information), so you can always guess based on the figure if you need to.
The way to approach a graph question is exactly the same as the way to approach a chart question. Follow the same three steps.
1.Read any text that accompanies the graph. It is important to know what the graph is showing and what scale the numbers are on.
2.Read the question.
3.Refer back to the graph and find the specific information you need.
This is how it works.
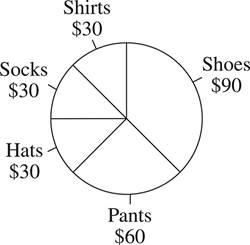
The graph in Figure 1 shows Emily’s clothing expenditures for the month of October. On which type of clothing did she spend the most money?
(A) Shoes
(B) Shirts
(C) Socks
(D) Hats
This one is easy. You can look at the pieces of the pie and identify the largest, or you can look at the amounts shown in the graph and choose the largest one. Either way, the answer is (A) because Emily spent more money on shoes than on any other clothing items in October.
Emily spent half of her clothing money on which two items?
(A) Shoes and pants
(B) Shoes and shirts
(C) Hats and socks
(D) Socks and shirts
Again, you can find the answer to this question two different ways. You can look for which two items together make up half the chart, or you can add up the total amount of money Emily spent ($240) and then figure out which two items made up half (or $120) of that amount. Either way is just fine, and either way, the right answer is (B), shoes and shirts.
PRACTICE DRILL 33—CHARTS AND GRAPHS
Questions 1—3 refer to the following summary of energy costs by district.
District |
2017 |
2021 |
A |
400 |
600 |
B |
500 |
700 |
C |
200 |
350 |
D |
100 |
150 |
E |
600 |
800 |
|
(All numbers are in thousands of dollars.) |
||
1.In 2021, which district spent twice as much on energy as District A spent in 2017?
2.Which district spent the most on electricity in 2017 and 2021 combined?
3.The total increase in energy expenditure in these districts, from 2017 to 2021, is how many dollars?
Questions 4 and 5 refer to the bar graph, which shows the number of cellphones owned by five students.
4.Carl owns as many cellphones as which two other students combined?
5.Which one student owns one-fourth of the cellphones accounted for in the bar graph?
Middle and Upper Levels Only
Questions 6—8 refer to Matt’s weekly time card, shown below.
Day |
In |
Out |
Hours Worked |
Monday |
2:00 p.m. |
5:30 p.m. |
3.5 |
Tuesday |
|||
Wednesday |
2:00 p.m. |
6:00 p.m. |
4 |
Thursday |
2:00 p.m. |
5:30 p.m. |
3.5 |
Friday |
2:00 p.m. |
5:00 p.m. |
3 |
Saturday |
|||
Sunday |
6.If Matt’s hourly salary is $6, what were his earnings for the week?
7.What is the average number of hours Matt worked on the days he worked during this particular week?
8.The hours that Matt worked on Monday accounted for what percent of the total number of hours he worked during this week?

When You Are Done
Check your answers in Chapter 3, this page.
You can make a chart to see how you’ve been doing!
REVIEW DRILL 2—THE BUILDING BLOCKS
1.If one-third of b is 15, then what is b ?
2.If 7x — 7 = 49, then what is x ?
3.If 4(y — 5) = 20, then what is y ?
4.8x + 1 < 65. Solve for x.
5.16 is what percent of 10 ?
6.What percent of 32 is 24 ?
7.What is the area of a triangle with base 7 and height 6 ?
(Middle and Upper Levels)
8.What is the diameter of a circle with an area of 49π ?
9.What is the radius of a circle with a circumference of 12π ?
10.What is the area of a circle with a diameter of 10 ?

When You Are Done
Check your answers in Chapter 3, this page.