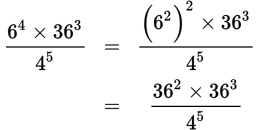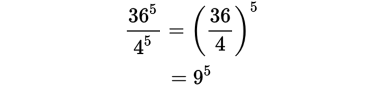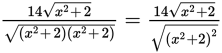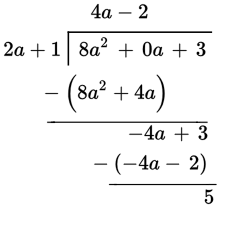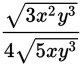PSAT/NMSQT Prep 2019 - Princeton Review 2019
Exponents, radicals, polynomials, and rational expressions and equations
Passport to advanced math
Math
CHAPTER OBJECTIVES
By the end of this chapter, you will be able to:
1. Simplify and solve expressions and equations involving exponents and/or radicals
2. Perform arithmetic operations on polynomials
3. Simplify expressions using polynomial long division and find polynomial remainders
4. Simplify and solve rational expressions and equations
5. Solve a formula for a given variable
SMARTPOINTS
|
Point Value |
SmartPoint Category |
|
80 Points |
Exponents |
Prepare
INTRODUCTION TO EXPONENTS AND RADICALS
We often turn to our calculators to solve difficult radical and exponent questions, especially in math-intensive classes. However, being too calculator dependent can cost you time and points on the PSAT. Further, on the PSAT, many radical and exponent questions are structured in such a way that your calculator can’t help you, even if it is allowed.
This chapter will review algebra and arithmetic rules that you may have learned at some point but likely haven’t used in a while. This chapter will reacquaint you with the formulas and procedures you’ll need to simplify even the toughest expressions and equations on the PSAT. We’ll start with exponents.
Questions involving exponents often look intimidating, but when you know the rules governing them, you’ll see that there are plenty of shortcuts. First, it’s important to understand the anatomy of a term that has an exponent. This term is comprised of two pieces: a base and an exponent (also called a power). The base is the number in larger type and is the value being multiplied by itself. The exponent, written as a superscript, shows you how many times the base is being multiplied by itself.
![]()
The following table lists the rules you’ll need to handle any exponent question you’ll see on the PSAT.
|
Rule |
Example |
|
When multiplying two terms with the same base, add the exponents. |
ab × ac = a(b+c) —> 42 × 43 = 42+3 = 45 |
|
When dividing two terms with the same base, subtract the exponents. |
|
|
When raising a power to another power, multiply the exponents. |
(ab)c = a(bc) —> (43)2 = 43×2 = 46; |
|
When raising a product to a power, apply the power to all factors in the product. |
(ab)c = ac × bc —> (2m)3 = 23 × m3 = 8m3 |
|
Any term raised to the zero power equals 1. |
a0 = 1 —> 40 = 1 |
|
A base raised to a negative exponent can be rewritten as the reciprocal raised to the positive of the original exponent. |
|
Note
Raising an expression involving addition or subtraction to a power, such as (a + b)2, requires a special process called FOIL, which you’ll learn about in chapter 6. You cannot merely distribute the exponent; this will certainly lead you to a trap answer.
Different things happen to different kinds of numbers when they are raised to powers. Compare the locations and values of the variables and numbers on the following number line to the results in the table for a summary.
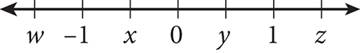
|
Quantity |
Even Exponent Result |
Odd Exponent Result |
Example |
|
w |
positive, absolute value increases |
negative, absolute value increases |
(—5)2 = 25; (—5)3 = —125 |
|
—1 |
always 1 |
always —1 |
n/a |
|
x |
positive, absolute value decreases |
negative, absolute value decreases |
|
|
0 |
always 0 |
always 0 |
n/a |
|
y |
positive, absolute value decreases |
positive, absolute value decreases |
|
|
1 |
always 1 |
always 1 |
n/a |
|
z |
positive, absolute value increases |
positive, absolute value increases |
32 = 9; 33 = 27 |
1. Which expression is equivalent to ![]() ?
?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Use the Kaplan Method for Math to solve this question, working through it step-by-step. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to find the expression that is equivalent to the one given. |
|
|
Step 2: Choose the best strategy to answer the question What’s the first step in simplifying this expression? Follow the order of operations. Cube each term within the parentheses, then simplify. |
|
|
Step 3: Check that you answered the right question Choice (A) is a match. |
Note
Once you get to ![]() , there are no like bases or exponents, so your work is done.
, there are no like bases or exponents, so your work is done.
2. Which of the following has the same value as ![]() ?
?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You’re asked to identify the expression that has the same value as the one presented; this means you need to simplify it. |
|
|
Step 2: Choose the best strategy to answer the question As written, you can’t combine the bases or the exponents. However, 36 = 62, so rewrite the numerator to reflect this relationship. Then combine the bases in the numerator by adding the exponents. The bases are now being raised to the same power, 5, so rewrite the expression using a single exponent. Then simplify by dividing. |
|
|
Step 3: Check that you answered the right question Although 95 is correct, it’s not one of the answer choices, so you’ll need to simplify even further. Rewrite 9 as 32 and then use exponent rules to simplify. The result is 310, which is (B). |
|
Note
A calculator could probably handle numbers the size of those in the previous question, but what if the question is in the no calculator section? Knowing exponent rules for Test Day is critical.
RADICALS
A radical can be written using a fractional exponent. You can think of addition and subtraction (and multiplication and division) as opposites; similarly, raising a number to a power and taking the root of the number are another opposite pair. Specifically, when you raise a term to the nth power, taking the nth root will return the original term. Consider, for example, 34 = 3 × 3 × 3 × 3 = 81. If you take the fourth root of 81 (that is, determine the number that can be multiplied by itself four times to get 81), you will arrive at the original term: ![]() .
.
Radicals can be intimidating at first, but remembering the basic rules for radicals can make them much easier to tackle. The following table contains all the formulas you’ll need to know to achieve “radical” success on the PSAT.
|
Rule |
Example |
|
When a fraction is under a radical, you can rewrite it using two radicals: one containing the numerator and the other containing the denominator. |
|
|
Two factors under a single radical can be rewritten as separate radicals multiplied together. |
|
|
A radical can be written using a fractional exponent. |
|
|
When you have a fractional exponent, the numerator is the power to which the base is raised, and the denominator is the root to be taken. |
|
|
When a number is squared, the original number can be positive or negative, but the square root of a number can only be positive. |
If a2 = 81, then a = ±9, BUT |
Note
Note this difference: by definition, the square root of a number is positive. However, when you take the square root to solve for a variable, you get two solutions: one that is positive and one that is negative. For instance, by definition ![]() . However, if you are solving x 2 = 4, x will have two solutions: x = ±2.
. However, if you are solving x 2 = 4, x will have two solutions: x = ±2.
It is not considered proper notation to leave a radical in the denominator of a fraction. However, it’s sometimes better to keep them through intermediate steps to make the math easier (and sometimes the radical is eliminated along the way). Once all manipulations are complete, the denominator can be rationalized to remove a remaining radical by multiplying both the numerator and denominator by that same radical.
|
1. Original Fraction |
2. Rationalization |
3. Intermediate Math |
4. Resulting Fraction |
|
|
|
|
|
|
|
|
|
|
Sometimes, you’ll have an expression such as ![]() in the denominator. To rationalize this, multiply by its conjugate, which is found by negating the second term; in this case, the conjugate is
in the denominator. To rationalize this, multiply by its conjugate, which is found by negating the second term; in this case, the conjugate is ![]() .
.
As a general rule of thumb, you are not likely to see a radical in the denominator of the answer choices on the PSAT, so you’ll need to be comfortable with rationalizing expressions that contain radicals.
Note
When you rationalize a denominator, you are not changing the value of the expression; you’re only changing the expression’s appearance. This is because the numerator and the denominator of the fraction that you multiply by are the same, which means you’re simply multiplying by 1.
Ready to take on a test-like question that involves radicals? Take a look at the following:
3. If ![]() , what is the value of x + 4 ?
, what is the value of x + 4 ?
1. 629
2. 1,300
3. 1,628
4. 2,405
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go All you need to do is solve for x. |
|
|
Step 2: Choose the best strategy to answer the question What should you do first? Solving a radical equation is similar to solving a linear equation, so start by isolating the variable term on one side. What operation will remove the root from the left side of the equation? To undo the radical, apply the exponent that corresponds to the root (4 in this case) to each side. |
|
|
Step 3: Check that you answered the right question You’ve found x, so add 4 and you’ll be done. The correct answer is (B). |
x + 4 = 1,300 |
POLYNOMIALS
By now you’re used to seeing equations, exponents, and variables; another important topic you are sure to see on the PSAT is polynomials. A polynomial is an expression comprised of variables, exponents, and coefficients, and the only operations involved are addition, subtraction, multiplication, division (by constants only), and nonnegative integer exponents. A polynomial can have one or multiple terms. The following table contains examples of polynomial expressions and non-polynomial expressions.
|
Polynomial |
23x 2 |
|
|
47 |
|
Not a Polynomial |
|
x 3y −6 |
|
|
Note
Remember that a constant, such as 47, is considered a polynomial; this is the same as 47x 0. Also, keep in mind that for an expression to be a polynomial, division by a constant is allowed, but division by a variable is not.
Identifying like terms is an important skill that will serve you well on Test Day. To simplify polynomial expressions, you combine like terms just as you did with linear expressions and equations (x terms with x terms, constants with constants). To have like terms, the types of variables present and their exponents must match. For example, 2xy and −4xy are like terms; x and y are present in both and their corresponding exponents are identical. However, 2x 2y and 3xy are not like terms because the exponents on x do not match. A few more examples follow:
|
Like terms |
7x, 3x, 5x |
3, 15, 900 |
xy2, 7xy2, —2xy2 |
|
Not like terms |
3, x, x 2 |
4x, 4y, 4z |
xy 2, x 2y, 2xy |
You can also evaluate a polynomial expression (just like any other expression) for given values in its domain. For example, suppose you’re given the polynomial expression x 3 + 5x 2 + 1. At x = —1, the value of the expression is (—1)3 + 5(—1)2 + 1, which simplifies to —1 + 5 + 1 = 5.
A polynomial can be named based on its degree. For a single-variable polynomial, the degree is the highest power on the variable. For example, the degree of 3x 4 — 2x 3 + x 2 — 5x + 2 is 4 because the highest power of x is 4. For a multivariable polynomial, the degree is the highest sum of the exponents on any one term. For example, the degree of 3x 2y2 — 5x 2y + x 3 is 4 because the sum of the exponents in the term 3x 2y2 equals 4.
On Test Day, you might be asked about the nature of the zeros or roots of a polynomial. Simply put, zeros are the x-intercepts of a polynomial’s graph, which can be found by setting each factor of the polynomial equal to 0. For example, in the polynomial equation y = (x + 6)(x — 2)2, you would have three equations: x + 6 = 0, x — 2 = 0, and x — 2 = 0 (because x — 2 is squared, that binomial appears twice in the equation). Solving for x in each yields —6, 2, and 2; we say that the equation has two zeros: —6 and 2. Zeros can have varying levels of multiplicity, which is the number of times that a factor appears in the polynomial equation. In the preceding example, x + 6 appears once in the equation, so its corresponding zero (—6) is called a simple zero. Because x — 2 appears twice in the equation, its corresponding zero (2) is called a double zero.
You can recognize the multiplicity of a zero from the polynomial’s graph as well. Following is the graph of y = (x + 6)(x — 2)2:
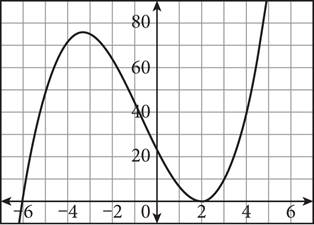
When a polynomial has a simple zero (multiplicity 1) or any zero with an odd multiplicity, its graph will cross the x-axis (as it does at x = —6 in the graph above). When a polynomial has a double zero (multiplicity 2) or any zero with an even multiplicity, it just touches the x-axis (as it does at x = 2 in the graph above).
Use your knowledge of polynomials to answer the following test-like question:
4. If A and B are polynomial expressions such that A = 24xy + 13 and B = 8xy + 1, how much greater is A than B ?
1. 32xy + 14
2. 16xy + 14
3. 16xy + 12
4. 32xy + 13
Use the Kaplan Method for Math to solve this question, working through it step-by-step. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go Don’t let the unusual wording fool you. To find how much greater A is, just do what you would do for two numbers: subtract the smaller from the larger. |
|
|
Step 2: Choose the best strategy to answer the question What’s your first step? Substitute the correct expressions for A and B. Distribute the —1 outside the second set of parentheses. Be careful here; this is an easy place to make a mistake. And afterward? Combine like terms. Rearranging so that like terms are next to each other helps here. |
(24xy + 13) — (8xy + 1) = 24xy + 13 — 8xy — 1 = 24xy — 8xy + 13 — 1 = 16xy + 12 |
|
Step 3: Check that you answered the right question No further simplification is possible; the correct answer is (C), so you’re done. |
Adding and subtracting polynomials are straightforward operations, but what about multiplying and dividing them? These operations are a little tougher but (fortunately) far from impossible.
Multiplying polynomials is just like multiplying ordinary numbers except you want to pay special attention to distributing and combining like terms. Take the expression (3x3 + 5x)(2x 2 + x −17) as an example. All you need to do is distribute each term in the first set of parentheses to each term in the second set. Distribute the 3x3 first, then repeat with 5x:

The following table shows the product for each step:
|
1 |
2 |
3 |
|
3x 3 • 2x 2 = 6x 5 |
3x 3 • x = 3x 4 |
3x 3 • (−17) = −51x 3 |
|
4 |
5 |
6 |
|
5x • 2x 2 = 10x 3 |
5x • x = 5x 2 |
5x • (−17) = −85x |
All that’s left to do now is write out the expression and combine any like terms:
6x 5 + 3x 4 — 51x3 + 10x3 + 5x 2 — 85x
= 6x 5 + 3x 4 — 41x 3 + 5x 2 — 85x
Although it is relatively straightforward to add, subtract, and multiply polynomials, dividing polynomial expressions requires a different, more involved process called polynomial long division. Polynomial long division is just like regular long division except, as the name suggests, you use polynomials in place of numbers.
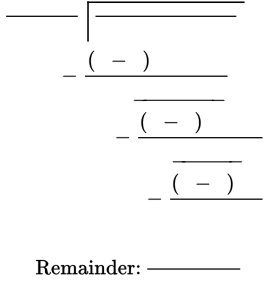
Suppose you want to divide x 3 + 3x + 7 by x + 4. You can set this up as a long division problem:
![]()
Notice that even though the dividend does not have an x 2 term, a placeholder is used to keep the terms organized. Because 0x 2 is equal to 0, adding this placeholder term doesn’t change the value of the polynomial. Start by dividing the first term of the dividend by the first term of the divisor to get x 2. Multiply the entire divisor by x 2 and subtract this product from the dividend:
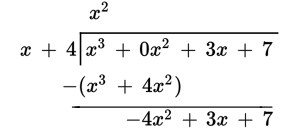
Continue by dividing the next term, −4x 2, by the first term of the divisor. Bring down leftover terms as needed. Multiply the quotient, −4x, by the entire divisor and then subtract:
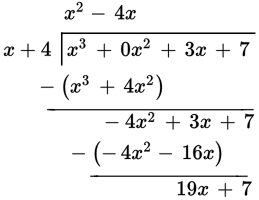
Finally, repeat this process with the 19x + 7:
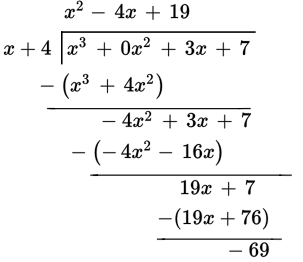
When all is said and done, the quotient is x 2 − 4x + 19 with a remainder of −69; the remainder is written over the divisor in a separate term. Thus, the final answer is ![]() .
.
This is a topic many students tend to forget soon after it’s tested in math class, so make sure you spend sufficient time brushing up on it.
Note
You can use polynomial long division to determine whether a binomial is a factor of a polynomial. If the remainder in the previous example had been 0, then x + 4 would have been a factor of the polynomial x 3 + 3x + 7.
Let’s try a polynomial long division question:
5. What is the remainder when 8a2 + 3 is divided by 2a + 1 ?
1. −5
2. −1
3. 1
4. 5
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You must find the remainder when 8a2 + 3 is divided by 2a + 1. |
|
|
Step 2: Choose the best strategy to answer the question |
|
|
Write as a polynomial long division problem. Once it’s set up, work carefully through each step until you get to the end. |
|
|
Step 3: Check that you answered the right question You get 5 for the remainder, which is (D). |
RATIONAL EXPRESSIONS
A rational expression is simply a ratio (or fraction) of polynomials. In other words, it is a fraction with a polynomial as the numerator and another polynomial as the denominator. The rules that govern fractions and polynomials also govern rational expressions, so if you know these well, you’ll be in good shape when you encounter one on Test Day.
There are a few important tidbits to remember about rational expressions; these are summarized here. They are also true for rational equations.
· For an expression to be rational, the numerator and denominator must both be polynomials.
· Like polynomials, rational expressions are also designated certain degrees based on the term with the highest variable exponent sum. For instance, the expression ![]() has a first-degree numerator and a second-degree denominator.
has a first-degree numerator and a second-degree denominator.
· Because rational expressions by definition can have polynomial denominators, they will often be undefined for certain values. For example, the expression ![]() is defined for all values of x except —2. This is because when x = —2, the denominator of the expression is 0, which would make the expression undefined.
is defined for all values of x except —2. This is because when x = —2, the denominator of the expression is 0, which would make the expression undefined.
· Factors in a rational expression can be canceled when simplifying, but under no circumstances can you do the same with individual terms. Consider, for instance, the expression ![]() . Many students will attempt to cancel the x 2, x, and 6 terms to give
. Many students will attempt to cancel the x 2, x, and 6 terms to give![]() , which is never correct. Don’t even think about trying this on Test Day.
, which is never correct. Don’t even think about trying this on Test Day.
· Like fractions, rational expressions can be proper or improper. A proper rational expression has a lower-degree numerator than denominator ![]() , and an improper one has a higher-degree numerator than denominator
, and an improper one has a higher-degree numerator than denominator ![]() . The latter can be simplified using polynomial long division.
. The latter can be simplified using polynomial long division.
Note
For those who are curious, the correct way to simplify ![]() is to factor, which you’ll learn about in chapter 10. For now, know that this equals
is to factor, which you’ll learn about in chapter 10. For now, know that this equals ![]() . Cancel the x + 2 factors to get
. Cancel the x + 2 factors to get ![]() .
.
SOLVING RATIONAL EQUATIONS
Rational equations are just like rational expressions except for one difference: they have an equal sign. They follow the same rules as rational expressions. The steps you take to solve the more friendly-looking linear equations apply to rational equations as well.
When solving rational equations, beware of extraneous solutions—solutions derived that don’t satisfy the original equation. This happens when the derived solution causes 0 in the denominator of any of the terms in the equation (because division by 0 is not possible). Take the equation ![]() , for instance. After multiplying both sides by the common denominator (x + 4)(x − 4), you have (x − 4) + (x + 4) = 8. Solving for x yields 2x = 8, which simplifies to x = 4. However, when 4 is substituted for x, you get 0 in the denominator of both the second and third terms of the equation, so 4 is an extraneous solution. Therefore, this equation is said to have no solution.
, for instance. After multiplying both sides by the common denominator (x + 4)(x − 4), you have (x − 4) + (x + 4) = 8. Solving for x yields 2x = 8, which simplifies to x = 4. However, when 4 is substituted for x, you get 0 in the denominator of both the second and third terms of the equation, so 4 is an extraneous solution. Therefore, this equation is said to have no solution.
Note
Whenever you encounter an equation with variables in a denominator or under a radical, make sure you check the solutions by plugging the values back into the original equation.
6. Which value of x satisfies the equation ![]() ?
?
1. −1
2. 1
3. 4
4. 5
Work through the Kaplan Method for Math step-by-step to solve this question. The following table shows Kaplan’s strategic thinking on the left, along with suggested math scratchwork on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You’re asked to determine which value of x satisfies the equation. |
|
|
Step 2: Choose the best strategy to answer the question |
|
|
Start by identifying a common denominator. By factoring x out of the denominator of the term on the right side of the equation, you’ll see that the common denominator across all three terms is x(x − 8). Multiply the entire equation by this expression, then distribute properly and solve for x. |
|
|
Step 3: Check that you answered the right question Because “no solution” is not a choice, you can be confident that 5 is not an extraneous solution. Choice (D) is therefore correct. |
Note
Extraneous solutions are solutions that cause the entire expression to become undefined. Look out for zeros in denominators and negatives under square roots.
MODELING REAL-WORLD APPLICATIONS USING POLYNOMIAL, RADICAL, AND RATIONAL EQUATIONS
A typical rational equation that models a real-world scenario (and that you’re likely to see on Test Day) involves rates. Recall from chapter 3 that distance is the product of rate and time (d = rt); this equation will serve you well when solving rational equations involving rates. In some cases, you may want to change d to W (for work), as some questions ask how long it will take to complete some kind of work or a specific task. The good news is that the math doesn’t change. For example, you can calculate a combined rate by rewriting W = rt as ![]() for each person (or machine) working on a job and then adding the rates together.
for each person (or machine) working on a job and then adding the rates together.
Here’s an example: Suppose machine A can complete a job in 2 hours and machine B can do the same job in 4 hours. You want to know how long it will take to do this job if both machines work together. Their rates would be ![]() job per hour and
job per hour and ![]() job per hour, respectively. The combined rate would be
job per hour, respectively. The combined rate would be ![]() job per hour, which means
job per hour, which means ![]() . Thus, it will take
. Thus, it will take ![]() hours to complete the job if A and B work together.
hours to complete the job if A and B work together.
Ready for a real-world example? Check out the next question:
7. Ankeet needs to back up a large quantity of financial data for his firm. He has access to two systems that can assist with the task. One system is three times as fast as the other. If Ankeet uses both systems together, the backup will be complete in 12 hours. If the equation ![]() represents the situation, what does
represents the situation, what does ![]() represent?
represent?
1. The time, in hours, that it takes the faster system to complete the full data backup when working alone
2. The portion of the data backup that the faster system will complete in 1 hour
3. The time, in hours, that it takes the slower system to complete the full data backup when working alone
4. The portion of the data backup that the faster system will complete in 3 hours
There’s no scratchwork for this question, but Kaplan’s strategic thinking is provided in the table. Follow along as we reason through the question to get the correct answer.
|
Strategic Thinking |
|
Step 1: Read the question, identifying and organizing important information as you go You must determine the significance of |
|
Step 2: Choose the best strategy to answer the question The left side of the equation shows the sum of the two systems’ task completion rates. A rate cannot also be a quantity of time, so eliminate A and C. To determine which remaining choice is correct, think carefully. When the machines work together, they complete the job in 12 hours; put another way, they complete |
|
Step 3: Check that you answered the right question The portion of the job that the faster system will complete in 1 hour is |
SOLVING A FORMULA OR EQUATION FOR A GIVEN VARIABLE
If you’ve ever taken a chemistry or physics course, you’ve probably noticed that many real-world situations can’t be represented by simple linear equations. There are frequently radicals, exponents, and fractions galore. For example, the root-mean-square velocity for particles in a gas can be described by the following equation:
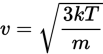
In this equation, v represents the root-mean-square velocity, k is the Boltzmann constant, T is the temperature in degrees Kelvin, and m is the mass of 1 molecule of the gas. It’s a great equation if you have k, T, and m and are looking for v. However, if you’re looking for a different quantity, having that unknown buried among others (and under a radical to boot) can be unnerving, but unearthing it is easier than it appears. Let’s say you’re given v, k, and m but need to find T. First, square both sides to eliminate the radical to yield ![]() . Next, isolate T by multiplying both sides by m and dividing by
. Next, isolate T by multiplying both sides by m and dividing by ![]() ; the result is
; the result is ![]() .
.
At this point, you can plug in the values of m, v, and k to solve for T. Sometimes the PSAT will have you do just that: solve for the numerical value of a variable of interest. In other situations, you’ll need to rearrange an equation so that a different variable is isolated. The same rules of algebra you’ve used all along apply. The difference: you’re manipulating solely variables.
Practice
Now you’ll have a chance to try a few more test-like questions. Some guidance is provided, but you’ll need to fill in the missing parts of explanations or the step-by-step math to get to the correct answer. Don’t worry—after going through the examples at the beginning of this chapter, these questions should be completely doable. If you’re still struggling, review the worked examples in this chapter.
8. A plasma is a gas composed of positively charged atom nuclei and negatively charged electrons. When a plasma is at equilibrium, the density of charge oscillates (shifts back and forth) at what is called the plasma frequency, which can be found using the following formula:
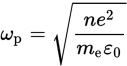
In the formula, n is the number of electrons present, e is electric charge, me is the mass of a single electron, and ε0 is permittivity of free space. Which of the following equations correctly shows the electric charge in terms of the other variables?
1. ![]()
2. 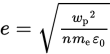
3. ![]()
4. ![]()
Use the scaffolding that follows as your map through the question. Kaplan’s strategic thinking is on the left, and bits of scratchwork are on the right. If you aren’t sure where to start, fill in the blanks in the table as you work from top to bottom.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to identify the equation that represents electric charge. Translation: solve the given equation for e. |
|
|
Step 2: Choose the best strategy to answer the question There are several variables and unusual symbols. How should this be solved? Don’t let the strange Greek letters intimidate you; just treat them as you would “normal” variables. Start by undoing the radical so you can get to what’s underneath, then isolate the correct variable. Related note: don’t panic if you’ve never heard of “permittivity of free space.” If you don’t need it to answer the question, don’t sweat it. |
______ = ______ ______ = ______ ______ = ______ |
|
Step 3: Check that you answered the right question Did you get (A)? If so, you’re absolutely correct. |
|
Note
Beware of look-alike variables; it’s easy to mistake ε0 for e in this question. Make sure you keep them straight in your scratchwork.
9. What is the value of the remainder when ![]() is divided by
is divided by ![]() ?
?

Use the scaffolding that follows as your map through the question. Kaplan’s strategic thinking is on the left, and bits of scratchwork are on the right. If you aren’t sure where to start, fill in the blanks in the table as you work from top to bottom.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to divide the first polynomial by the second. |
|
|
Step 2: Choose the best strategy to answer the question Can anything be factored out of the first polynomial? Possibly, but it would likely take time you don’t have. Polynomial long division will prevent wasted time. Fill in the blanks on the right to get to the answer. |
|
|
Step 3: Check that you answered the right question If your answer is 5, congrats! You’re correct. |
|
10.Which of the following is the correct simplification of ![]() ?
?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Use the scaffolding that follows as your map through the question. Kaplan’s strategic thinking is on the left, and bits of scratchwork are on the right.
|
Strategic Thinking |
Math Scratchwork |
|
Step 1: Read the question, identifying and organizing important information as you go You need to correctly simplify the given expression. |
|
|
Step 2: Choose the best strategy to answer the question There’s no real equation. What route should you take? Use your exponent and radical rules to get to the answer. You can remove squares from under the radical now, but there’s a faster route: split the numerator’s radical terms so each is under a separate radical; repeat with the denominator. Doing this makes cancelling easier and lessens the chance of making a careless error. Don’t forget to rationalize the denominator, if necessary. |
|
|
Step 3: Check that you answered the right question Did you get (B)? If so, you’re absolutely correct. |
|
Perform
Now that you’ve seen the variety of ways in which the PSAT can test you on the topics in this chapter, try the following questions to check your understanding. Give yourself 3.5 minutes to tackle the following three questions. Make sure you use the Kaplan Method for Math as often as you can. Remember, you want to emphasize speed and efficiency in addition to simply getting the correct answer.
11.The electromagnetic spectrum encompasses all types of light, both visible and invisible. A light’s wavelength is inversely proportional to its damage capability and can be found using the equation c = λν, where c is the speed of light in a vacuum in meters per second (3 × 109 m/s), λ (lambda) is wavelength in meters, and ν (nu) is frequency in reciprocal seconds (s—1). Suppose environmental scientists are scanning for ozone layer depletion and discover an unusually high concentration of ultraviolet light near Los Angeles. If this light has a wavelength of 150 nanometers (1 m = 1 × 109 nm), what is its frequency in s—1 ?
1. 2 × 107
2. 3 × 107
3. 2 × 1015
4. 3 × 1015
12.Which of the following expressions is equivalent to ![]() ?
?
1. ![]()
2. 1
3. 7
4. ![]()
13.If n3 = −8, what is the value of ![]() ?
?

On your own
1. Which of the following is equivalent to the expression ![]() ?
?
1. 0
2. 1
3. 3
4. 9
2. What is the resulting coefficient of x after multiplying —x + 4 by x — 5 ?
1. —9
2. —1
3. 1
4. 9
3. ![]()
Which of the following is equivalent to the expression above?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
4. The expression ![]() is equivalent to which of the following?
is equivalent to which of the following?
1. ![]()
2. 1
3. x
4. x 3
5. What is the quotient of ![]() ?
?
1. 2x + 1
2. 2x + 3
3. 4x + 3
4. 4x + 7
6. ![]()
The power generated by a windmill is related to the velocity of the wind by the equation shown above, where P is the power in watts and v is the wind velocity in miles per hour. What is the wind velocity when the windmill is generating 160 watts of power?
1. 20 mph
2. 32 mph
3. 64 mph
4. 89 mph
7. ![]()
The period of a pendulum is the amount of time that it takes for the pendulum to swing back and forth to complete one full cycle. The period t in seconds depends on the length L of the pendulum in feet and is defined by the equation above. Which equation defines the length of the pendulum in terms of its period?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
8. 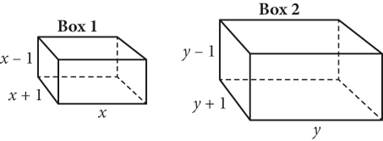
The length of Box 2 (y) shown above is twice the length of Box 1 (x). Which expression shows the difference in the volumes of the two boxes?
1. 2x 3 — 2x
2. 7x 3 — x
3. 7x 3 — 2x
4. 8 x 3 — 2x
9. If M = 12x 2 + 4x — 7 and N = 5x 2 — x + 8, then which of the following equals M — N ?
1. 7x 2 + 3x + 1
2. 7x 2 + 5x +1
3. 7x 2 + 3x — 15
4. 7x 2 + 5x — 15
10.The value of 6x + 5 is how much more than the value of 6x — 1 ?
1. 4
2. 6
3. 6x — 4
4. 6x + 6
11.Which of the following is the reduced form of ![]() ?
?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
12.What is the difference when ![]() is subtracted from
is subtracted from ![]() ?
?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
13.Which of the following represents ![]() as an integer?
as an integer?
1. 3
2. 9
3. 27
4. 81
14.When a liquid leaks onto a level surface, it generally spreads out equally in all directions, so the puddle is usually in the shape of a circle. When a hazardous chemical leaks like this, it is important to know how long it has been leaking to determine the possible risk to nearby water sources, vegetation, animals, and people. For a certain chemical, the equation ![]() , where d represents the diameter of the puddle in inches, can be used to find the number of minutes, m ≥ 1, that have passed since the leak began. If the diameter of a puddle created by a leak is 3 feet, about how many minutes has the liquid been leaking? (1 foot = 12 inches)
, where d represents the diameter of the puddle in inches, can be used to find the number of minutes, m ≥ 1, that have passed since the leak began. If the diameter of a puddle created by a leak is 3 feet, about how many minutes has the liquid been leaking? (1 foot = 12 inches)
1. 8
2. 15
3. 830
4. 2,026
15.For all a and b, what is the product of (a — b)2 and (a + b) ?
1. a2 — b2
2. a3 — b3
3. a3 — ab2 + a2b — b3
4. a3 — a2b — ab2 + b3
16.If A and B are given by A = 25x 2 + 10x − 45 and B = −12x 2 − 32x + 24, what is ![]() ?
?
1. 2x 2 — 6x — 3
2. 2x 2 — 6x + 20
3. 9x 2 — 10x — 15
4. 21x 2 + 22x — 39
17.If x > 1, then which of the following must be true?
1. ![]()
2. ![]()
3. ![]()
4. ![]()
18.If x > 4 and ![]() , then what is the value of x ?
, then what is the value of x ?