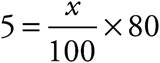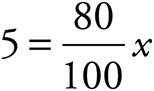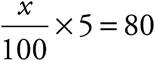PSAT/NMSQT Prep with Practice Tests - Princeton Review 2021

Math techniques
PSAT/NMSQT prep

In the previous chapter, we mentioned that one of the keys to doing well on the PSAT is to have a set of test-specific problem-solving skills. This chapter discusses some powerful strategies, which—though you may not use them in school—are specifically designed to get you points on the PSAT. Learn them well!

PLUGGING IN

One of the most powerful problem-solving skills on the PSAT is a technique we call Plugging In. Plugging In will turn nasty algebra questions into simple arithmetic and help you through the particularly twisted problems that you’ll often see on the PSAT. There are several varieties of Plugging In, each suited to a different kind of question.

Plugging In Your Own Numbers

The problem with doing algebra is that it’s just too easy to make a mistake.

Whenever you see a question with variables in the answer choices, use Plugging In.

Start by picking a number for the variable in the question (or for more than one variable, if necessary), solve the problem using your number, and then see which answer choice gives you the correct answer.

Take a look at the following question.

13.If 2x + x + = y, what is the value of xy − 1, in terms of x?

A)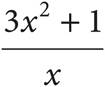

B)3x² − 1

C)3x² + 1

D)3x²

When to Plug In

· phrases like “in terms of” or “equivalent form” in the question

· variables in the question and/or answer choices

Here’s How to Crack It

The question asks for the value of xy − 1 in terms of x. Let’s try to avoid the algebra by plugging in. First, start by choosing a value for one of the variables. Here, all the action is happening to the x, so choose a value for x. Make x = 2. Next, work the question in Bite-Sized Pieces until you’ve come up with a numerical answer for the question. If x = 2, then the equation becomes 2(2) + 2 + = y. Multiply; then add on the left side: 4 + 2 + = y; = y. Note the question doesn’t want the value of y, but rather xy − 1. Because x = 2 and y = 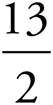, xy − 1 = (2) − 1 = 13 − 1 = 12. This is the target number; circle it.

Now that you have a target number, work your answer choices using Process of Elimination. Make x = 2 in each answer choice and eliminate any choice that doesn’t equal your target number of 12:

A)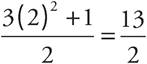 Not 12; eliminate!

B)3(2)² −1 = 11 Not 12; eliminate!

C)3(2)² + 1 = 13 Not 12; eliminate!

D)3(2)² = 12 Is 12; keep!

Only (D) matches your target number, so it must be the answer!

As you can see, Plugging In can turn messy algebra questions into more straightforward arithmetic questions. This technique is especially powerful when the PSAT asks you to find the equivalent form of an expression.

16.The expression x² + 4x − 4 is written in the equivalent form N² − 8. What is the value of N?

A)x² + 4x − 4

B)x² + 4x + 4

C)x − 2

D)x + 2

Plugging In: Quick Reference

·  When you see in terms of or equivalent form and there are variables in the answer choices, you can Plug In.

·  Pick your own number for an unknown in the question.

·  Do the necessary math to find the answer you’re shooting for, which is the target number. Circle the target number.

·  Use POE to eliminate every answer that doesn’t match the target number.

Here’s How to Crack It

The question asks for the value of N given two equivalent expressions. The variable x is all over the place, so assign a value for x. Try x = 2. Next, work the problem in Bite-Sized Pieces. The first expression becomes 2² + 4(2) − 4 = 4 + 8 − 4 = 8. The question then states that this is “written in the equivalent form” of N² − 8. If these expressions are equivalent, then N² − 8 must also equal 8. So set it equal to 8 and solve for N: N² −8 = 8; N²= 16; N = ± 4. The question is asking for N, so you’re looking for any answer that equals either −4 or 4 (because there are two possible values). These are your target numbers; circle them. Make x = 2 in each answer choice and eliminate any option that doesn’t match one of the target numbers:

A)2² + 4(2) − 4 = 4 + 8 − 4 = 8 Not −4 or 4; eliminate!

B)2² + 4(2) + 4 = 4 + 8 + 4 = 16 Not −4 or 4; eliminate!

C)2 − 2 = 0 Not −4 or 4; eliminate!

D)2 + 2 = 4 Yes!

The answer is (D).

Plugging In is such a great technique because it turns hard algebra questions into medium and sometimes even easy arithmetic questions. Remember this when you’re thinking of your POOD and looking for questions to do among the hard ones; if you see variables in the answers, there’s a good chance it’s one to try.

Don’t worry too much about what numbers you choose to plug in; just plug in easy numbers (small numbers like 2, 5, or 10 or numbers that make the arithmetic easy, like 100 if you’re looking for a percent). Also, be sure your numbers fit the conditions of the questions (for example, if they say x ≤ 11, don’t plug in 12).

What If There’s No Variable?

Sometimes you’ll see a question that doesn’t contain an x, y, or z, but which contains a hidden variable. If your answers are percents or fractional parts of some unknown quantity (total number of marbles in a jar, total miles to travel in a trip), try Plugging In.

Take a look at this question.

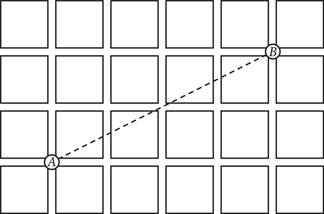
27.A neighborhood is comprised of square blocks, as shown above. Genna launches a drone from point A. The drone flies directly to point B, as shown by the dotted line. Genna then walks from point A to point B by following the streets by the shortest route possible. By approximately what percent was the distance Genna walked greater than the distance the drone flew?

A) 25%

B) 34%

C) 75%

D)134%

Here’s How to Crack It

The question asks for a comparison of the distance Genna walked to the distance the drone flew. No actual values are given, but the question deals with a relationship between numbers, so pick a number for the unknown value. Plug in for the size of the blocks. Assume each block is 1 unit by 1 unit. Genna must travel 4 blocks east and 2 blocks north, so she must travel 6 units total. (Note that it doesn’t matter whether she goes north then east, east then north, or a zigzag pattern from A to B; the shortest path will always be 6 units.)

To find the distance the drone travels, make a right triangle with legs 4 units (the distance east) and 2 units (the distance north). Find the hypotenuse (which is the direct distance from A to B) using the Pythagorean Theorem. The Pythagorean Theorem is a² + b² = c², where c is the hypotenuse. Therefore, 4² + 2² = c²; 16 + 4 = c²; 20 = c²; .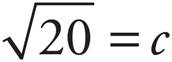

We’ll cover the Pythagorean Theorem in more detail in Chapter 14.

To find the percent difference, use the formula 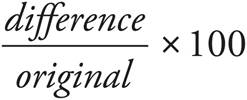. Because you want percent greater, the original is the smaller value (in this case 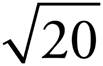): 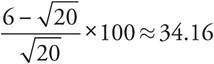, which is closest to (B).

Try another one.

Ratio of Students in a Club

16.The two-way table above shows the ratio of males and females and juniors and seniors in a particular club. If a male is chosen at random, what is the probability that he will be a junior?

A)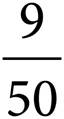

B)

C)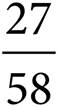

D)

We’ll cover probability in more detail later in this chapter.

Here’s How to Crack It

The question asks for the probability that a male chosen at random will be a junior. The total ratio of students is 1.00, so plug in for the total number of students. Make the number of students 100. To find the number of students in each category, you only need to multiply each number in the table by 100. This gives you the following:

You’re asked to find the probability of choosing a junior if you choose from the males. Probability is 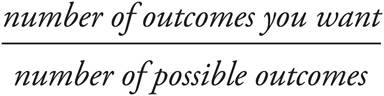. There are 18 male juniors and 42 total males, making the probability of choosing a junior from the males 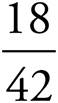, which reduces to . This matches (B).

Drill 1

Click here to download a PDF of Chapter 12 Drill 1.

Answers can be found in Part IV.

5.David acquired a data plan for his smart phone. Every month he pays a flat rate of $25 and an additional $0.05 for every megabyte he goes over his monthly limit. Which of the following represents David’s monthly data bill when he goes over his limit by m megabytes?

A)25 + 1.05m

B)25 + 0.05m

C)0.05(25 + m)

D)1.05(25 + m)

4.If 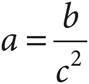and c ≠ 0, what is the value of ?

A)ac²

B)a²c⁴

C)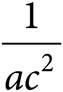

D)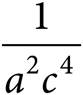

11.Luciano measured the amount of water that evaporated over a period of time from a container holding w ounces of water, where w is greater than 12. By the end of the first day, the cup had lost 2 ounces of water. By the end of the 7th day, the cup had lost an additional 8 ounces of water. By the end of the 11th day, the cup had lost half of the water that remained after the 7th day. Which of the following represents the remaining amount of water, in ounces, in Luciano’s container at the end of the 11th day?

A)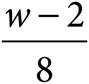

B) 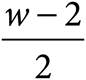− 10

C) w − 10

D)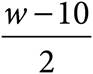

7.If p ≠ 0, what is the value of ?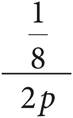

A)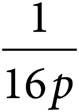

B)

C)

D) 4p

9.A certain standardized test has 50 questions. A student receives 1 point for each correct answer and loses of a point for each incorrect answer. Which of the following equations best models the net score, S, in points, for a student who completes all 50 questions and answers c of the questions correctly?

A)S = 50 − 0.25c

B)S = 50 − 0.75c

C)S = c − 0.25(50 − c)

D)S = c − 0.75(50 − c)

18.Jodi has x dollars in her bank account. She withdraws of the money in her account to pay her rent and another of the money in her account to make her car payment. Jodi then deposits her paycheck of y dollars into her account. A week later, she withdraws of the money in her account to spend on a new set of knives. In terms of x, how many dollars are left in Jodi’s account?

A)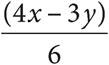

B)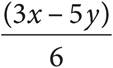

C)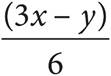

D)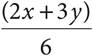

2 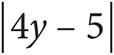< 24

12.What is the sum of all the integer solutions to the inequality above?

A) 7

B) 9

C)10

D)14

29.15% of the members of the incoming freshmen class at a certain university are left-handed, and the remaining members are right-handed. 65% of the same incoming freshmen class are female, and the rest are male. If of the left-handed students are male, then what percent of the female class is right-handed, to the nearest tenth of a percent? (Disregard the percent sign when gridding your answers. For example, if the answer is 43.2%, grid in 43.2.)

PLUGGING IN THE ANSWERS (PITA)

You can also plug in when the answer provided to a question is an actual value, such as 2, 4, 10, or 20. Why would you want to do a lot of complicated algebra to solve a question, when the answer is right there on the page? All you have to do is figure out which choice it is.

How can you tell which is the correct answer? Try every choice until you find the one that works. Even if this means you have to try all four choices, PITA is still a fast and reliable means of getting the right answer.

If you work strategically, however, you almost never need to try all four answers. If the question asks for either the greatest or the least answer, start there. Otherwise, start with one of the middle answer choices. If that answer works, you’re done. If the answer you started with was too big, try a smaller answer. If the answer you started with was too small, try a bigger answer. You can almost always find the answer in two or three tries this way. Let’s try PITA on the following question.

4.If the average (arithmetic mean) of 8 and x is equal to the average of 5, 9, and x, what is the value of x?

A)1

B)2

C)4

D)8

PITA = Plugging In the Answers

Don’t try to solve problems like this by writing equations and solving for x or y. Plugging In the Answers lets you use arithmetic instead of algebra, so you’re less likely to make errors.

Here’s How to Crack It

The question asks for the value of x based on an average. Rather than doing complicated algebra, try out the answers. Let’s start with (C) and plug in 4 for x. The question now reads:

If the average (arithmetic mean) of 8 and 4 is equal to the average of 5, 9, and 4…

Does this work? The average of 8 and 4 is 6, and the average of 5, 9, and 4 is also 6. Therefore, (C) is the answer.

Neat, huh? Of course, the first answer you choose won’t always be the correct one. Let’s try one more.

10.If (x − 2)² = 2x − 1, which of the following is a possible value of x?

A)1

B)2

C)3

D)6

Here’s How to Crack It

The question asks for the value of x, and there are numbers in the answer choices. Try plugging in the answers any time the question asks for a specific value like this. If we try plugging in (C), 3, for x, the equation becomes 1 = 5, which is false. So (C) can’t be right. If you’re not sure which way to go next, just pick a direction. It won’t take very long to figure out the correct answer. If we try plugging in (B), 2, for x, the equation becomes 0 = 3, which is false. If we try plugging in (A), 1, for x, the equation becomes 1 = 1, which is true. There’s no need to try other answers because there are no variables in the answers; only one answer choice can work. So the answer is (A).

Drill 2

Click here to download a PDF of Chapter 12 Drill 2.

Answers can be found in Part IV.

2(n + 5) = 3(n − 2) + 8

3.In the equation above, what is the value of n?

A)1

B)3

C)4

D)8

8.If 3^{x + 2} = 243, what is the value of x?

A)1

B)2

C)3

D)4

2x − y > −3

4x + y < 5

y > −6

7.Which of the following points is in the solution set of the system of inequalities above?

A)(−4, −1)

B)(−3, −2)

C)(−1, −1)

D)(3, −5)

10.If 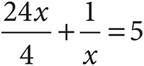, what is the value of x?

A)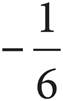

B)

C)

D)

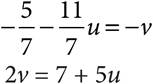
20.Based on the system of equations above, what is the value of v?

A)−4

B)−3

C)−1

D) 0

25.An alloy needs to contain between 10 and 15% of titanium. Which of the following inequalities represents the amount in kilograms, x, of a 20% titanium alloy that should be mixed with a 5% titanium alloy to produce 10 kilograms of an alloy with the acceptable percentage of titanium?

A)1.33 ≤ x ≤ 1.67

B)2.25 ≤ x ≤ 3.25

C)3.33 ≤ x ≤ 6.67

D)7.25 ≤ x ≤ 9.75

DATA ANALYSIS

In the calculator-allowed Math section (Section 4), there will be questions that will ask you to work with concepts such as averages, percentages, and unit conversions. Luckily, The Princeton Review has you covered! The rest of this chapter will give you techniques and strategies to help you tackle these questions.

Averages and T = AN

You probably remember the average formula from math class, which says Average (arithmetic mean) = 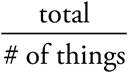. However, the PSAT rarely will ask you to take a simple average. Of the three parts of an average problem—the average, the total, and the number of things—you’re usually given the average and the number of things, and you’ll need to use the total to answer the question. If you multiply both sides of the average formula by the number of things, you get (average) × (# of things) = total. You can remember this as T = AN. Plug the information into the formula and solve.

Total

When calculating averages, always find the total. It’s the one piece of information that PSAT loves to withhold.

Let’s try this example.

9.The average (arithmetic mean) of 3 numbers is 22 and the smallest of these numbers is 2. If the remaining two numbers are equal, what are their values?

A)22

B)32

C)40

D)64

Here’s How to Crack It

The question gives the value of one number and the average of all three numbers and asks for the value of the two remaining numbers. Use T = AN. The average is 22, and there are 3 numbers. Therefore, T = (22)(3), so T = 66. If the smallest number is 2, the remaining two numbers equal 66 − 2 = 64. Finally, the remaining two numbers are equal, so divide: 64 ÷ 2 = 32. The answer is (B).

Try one more.

8.Caroline scored 85, 88, and 89 on three of her four history tests. If her average (arithmetic mean) score for all four tests was 90, what did she score on her fourth test?

A)90

B)93

C)96

D)98

Here’s How to Crack It

The question asks for the score Caroline received on her fourth test. Let’s start with what we know: we know that the average of all four of her tests was 90. Putting these into the formula T = AN gives us T = (90)(4), which means the total is 360. Since three of these tests have a sum of 85 + 88 + 89, or 262, we know that the score on the fourth test must be equal to 360 − 262, or 98. This makes the answer (D).

Median and Mode

Another two terms that are often tested along with average are median and mode.

The median of a group of numbers is the number in the middle, just as the “median” is the large divider in the middle of a road. To find the median, here’s what you do:

·  First, put the elements in the group in numerical order from lowest to highest.

·  If the number of elements in your group is odd, find the number in the middle. That’s the median.

·  If you have an even number of elements in the group, find the two numbers in the middle and calculate their average (arithmetic mean).

Finding a Median

To find the median of a set containing an even number of items, take the average of the two middle numbers after putting the numbers in order.

Try this on the following question.

3.If the 5 students in Ms. Jaffray’s math class scored 91, 83, 84, 90, and 85 on their final exams, what is the median score for her class on the final exam?

A)84

B)85

C)86

D)88

Here’s How to Crack It

First, let’s place these numbers in order from lowest to highest: 83, 84, 85, 90, 91. There are an odd number of elements in the group, and the number in the middle is 85, so the median of this group is 85 and the answer is (B).

The mode of a group of numbers is the number that appears the most. (Remember: mode sounds like most.) To find the mode of a group of numbers, simply see which element appears the greatest number of times.

28.An English professor graded the final papers of the 50 students in her Honors courses and recorded the information in the frequency table above. For this data, how much greater is the mode than the median?

Here’s How to Crack It

The question asks for the difference between the mode and the median of a list of data. On a frequency table, the mode is easy to see—it is the data with the greatest number in the Frequency column. On this table, the greatest number in that column is 11, and it is associated with the score of 91. Therefore, the mode is 91. The median is a little more difficult to find. You don’t want to take the time to list out all 50 scores, but the median will be the average of the 25th and 26th scores. If you can find those, you are all set. Start at the top of the chart and add up the numbers in the Frequency column till you get to 25. The first three scores, 85—87, account for 4 + 2 + 6 = 12 of the students. The scores of 88 and 89 account for another 3 + 4 = 7 students, so now we are up to the 19th student on the list. The next 7 students received a score of 90, so the 25th and 26th scores are both 90. The average of 90 and 90 is 90, so the median is 90. The difference between the mode and the median is 91 − 90 = 1. This is the correct answer.

Range

Another measure of the spread of data is range. The range of a list of numbers is the difference between the greatest number on the list and the least number on the list. For the list 4, 5, 5, 6, 7, 8, 9, 10, 20, the greatest number is 20 and the least is 4, so the range is 20 − 4 = 16.

Let’s look at a question.

25.A group of patients is recruited for a clinical trial. Their heights, recorded in centimeters, are listed in the table above. Two more patients are recruited to the study. After these patients join, the range of the heights is 42 cm. Which of the following could NOT be the heights of the two new patients?

A)154 cm and 186 cm

B)146 cm and 179 cm

C)150 cm and 188 cm

D)148 cm and 185 cm

Here’s How to Crack It

The question asks for the values that cannot be the heights of two new patients given information about the range of the data. To determine the current range, take the difference of the greatest and least values: 190 − 148 = 42 cm. If the range is to remain 42 cm, then the new patients’ heights cannot be greater than 190 cm or less than 148 cm tall. Choice (B) violates this restriction. Because the question wants what could NOT be the heights of the new patients, the answer is (B).

PROBABILITY

Probability refers to the chance that an event will happen, and it is given as a percent or a fractional value between 0 and 1, inclusive. A probability of 0 means that the event will never happen; a probability of 1 means that it is certain to happen.

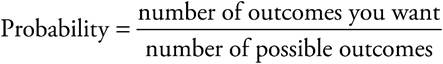
For instance, if you have a die with faces numbered 1 to 6, what is the chance of rolling a 2? There is one face with the number 2 on it, out of 6 total faces. Therefore, the probability of rolling a 2 is .

What is the chance of rolling an even number on one roll of this die? There are 3 faces of the die with an even number (the sides numbered 2, 4, and 6) out of a total of 6 faces. Therefore, the probability of rolling an even number is , or .

Let’s look at how this concept will be tested on the PSAT.

18.A survey was conducted among a randomly chosen sample of full-time salaried workers about satisfaction in their current jobs. The table below shows a summary of the survey results.

Reported Job Satisfaction by Education Level (in thousands)

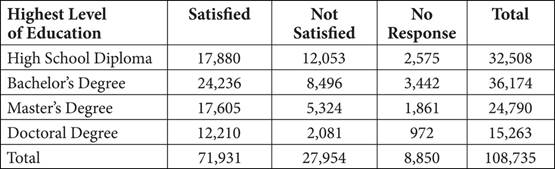
All persons who have earned a Master’s or Doctoral degree must have previously earned a Bachelor’s degree. What is the probability that a full-time salaried worker does NOT have a Bachelor’s degree?

A)29.9%

B)33.3%

C)36.8%

D)66.7%

Here’s How to Crack It

The question asks for the probability that a full-time worker does not have a Bachelor’s degree.

If everyone with a Master’s or Doctoral degree has a Bachelor’s degree, then the only people who do NOT have a Bachelor’s degree are those whose highest level of education is a High School Diploma. Find the probability of choosing someone with a High School Diploma out of the total: 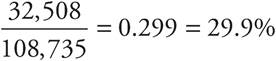, which is (A).

Rates

Rate is a concept related to averages. Cars travel at an average speed. Work gets done at an average rate. Because the ideas are similar, you can use Distance = Speed × Time (D = ST) or Work = Rate × Time (W = RT) to tackle these problems.

Of course, you might use the simple definitions of speed or rate to answer some questions.

Problem: If a fisherman can tie 9 flies for fly fishing in an hour and a half, how long does it take him to tie one fly, in minutes?

Solution: First, convert the hour and a half to 90 minutes so your units are consistent. Since Work = Rate × Time, the definition of rate is 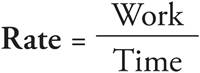. Divide 9 by 90 to get the rate, 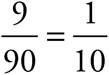, or one fly every 10 minutes.

Let’s look at an example of a PSAT rate question.

28.Sally, Abdul, and Juanita have volunteered to stuff a certain number of envelopes for a local charity. Working by herself, Sally could stuff all the envelopes in exactly 3 hours. Working by himself, Abdul could stuff all the envelopes in exactly 4 hours. Working by herself, Juanita could stuff all the envelopes in exactly 6 hours. If Sally, Abdul, and Juanita work together at these rates to stuff all the envelopes, what fraction of the envelopes will be stuffed by Juanita?

Here’s How to Crack It

The question asks for the fraction of the envelopes Juanita will stuff when she works together with two others, all at different rates. Since the question doesn’t tell you how many envelopes to stuff, this is a great question to plug in on. Because Sally takes 3 hours, Abdul takes 4 hours, and Juanita takes 6 hours, you want to choose a multiple of all those numbers. Make the total number of envelopes to stuff 120. Next, use the definition of rate to find each person’s rate. Sally stuffs 120 envelopes in 3 hours, so her rate is 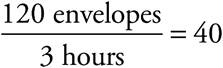envelopes per hour. Similarly, Abdul’s rate is 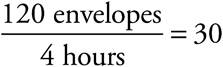envelopes per hour, and Juanita’s rate is 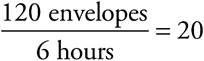envelopes per hour.

If all three people work together, their total rate will be 40 + 30 + 20 = 90 envelopes/hour. During that hour Juanita will stuff 20 envelopes, meaning she does 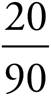, or , of the job.

PERCENTS

Percent just means “divided by 100.” So 20 percent = 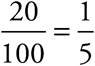, or .2.

Likewise, 400 percent =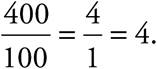

Any percent question can be translated into algebra—just use the following rules:

Take a look at some examples of phrases you might have to translate on the PSAT:

Percent Increase/Decrease

Percent Increase or Percent Decrease =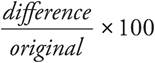

For example, if an $80 item is reduced to $60 during a sale, the percent decrease is the change in price ($80 − $60 = $20) divided by the original amount ($80), which gives us .25. Multiply by 100 to get 25 percent.

Try a question.

Estimated Numbers of Cell Phone Users by Type (in millions)

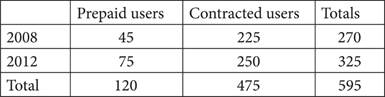
26.By how much greater was the percent increase in prepaid users from 2008 to 2012 than the percent increase in contracted users over the same period, to the nearest percent?

A) 6%

B)10%

C)30%

D)56%

Looking for More Practice?

Check out our 550+ PSAT Practice Questions, 2nd Edition!

Here’s How to Crack It

The question asks for a comparison of the percent increase in prepaid users over time to the percent increase in contracted users over time. First, find the percent increase in each group. Remember that percent increase is 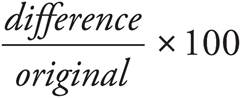. For prepaid users, the equation would be 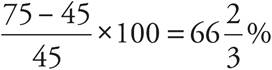. Contracted users: 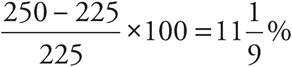. Finally, subtract: 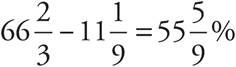, which is closest to (D).

GROWTH AND DECAY

Another aspect of percent questions may relate to things that increase or decrease by a certain percent over time. This is known as “growth and decay.” Real-world examples include population growth, radioactive decay, and credit payments, to name a few. While Plugging In can help on these, it is also useful to know the growth and decay formula.

When the growth or decay rate is a percent of the total population:

final amount = original amount (1 ± rate)^{number of changes}

Let’s see how this formula can make quick work of an otherwise tedious question.

14.The population of Bethesda, Maryland is currently 61,000 and is growing at a rate of 2.5% every three months. If Bethesda’s population, P, is a function of time in years, t, then which of the following functions represents the town’s population growth?

A)P(t) = 61,000(1.025)^t

B)P(t) = 61,000(1.1)^t

C)P(t) = 61,000(1.025)^4t

D)P(t) = 61,000(1.1)^3t

Here’s How to Crack It

The question asks for a function to represent population growth over time. Carefully translate the information in the question in Bite-Sized Pieces. Because the rate of growth is 2.5%, you need to add 0.025 (2.5% in decimal form) to 1 within the parenthesis. This would be 1 + 0.025 = 1.025. Eliminate (B) and (D) because they do not have this piece. The only difference between (A) and (C) is the exponent, which represents the number of changes. Here, t is in years, but the population increases every 3 months, which is 4 times a year. This means you want 4 changes when t = 1; this gives you (C) as your answer.

RATIOS AND PROPORTIONS

Some questions in the calculator-allowed Math section (Section 4) will ask about ratios and proportions. With the strategies that you’ll learn on the next few pages, you’ll be well prepared to tackle these concepts on the PSAT.

Ratios

Ratios are about relationships between numbers. Whereas a fraction is a relationship between a part and a whole, a ratio is about the relationship between parts. So, for example, if there were 3 boys and 7 girls in a room, the fraction of boys in the room would be . But the ratio of boys to girls would be 3:7 or . Notice that if you add up the parts, you get the whole: 7 + 3 = 10. That’s important for PSAT ratio questions, and you’ll see why in a moment.

Ratio questions usually aren’t difficult to identify. The question will tell you that there is a “ratio” of one thing to another, such as a 2:3 ratio of boys to girls in a club. Often, the PSAT will ask you to compare different ratios or to find the greatest or least ratio. To do so, divide the first part of the ratio by the second and compare the resulting values.

Gridding In

A ratio is usually expressed as 2:3 or 2 to 3, but if you need to grid a ratio, grid it as .

Try this one.

5.The ice cream flavor preferences of a randomly selected group of young Americans aged 3—18 are represented in the table below. Survey participants were asked to choose their favorite flavor among the following five: Vanilla, Chocolate, Mint Chocolate Chip, Cookies and Cream, and Coffee.

Reported favorite ice cream flavor by age group

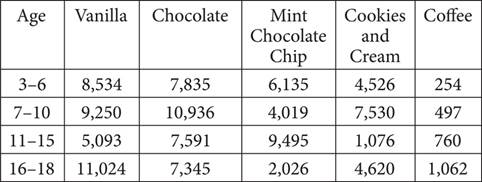
According to the data in the table above, the ratio of the most- to least-favorite flavors among the 7—10 age group is approximately how many times greater than the ratio of the most- to least-favorite flavors among the 11—15 age group?

A)1.8

B)3.4

C)4.2

D)6.7

Here’s How to Crack It

The question asks for a comparison of two ratios based on the data in the table. First, you need to find the ratio of the most- to least-favorite flavor for each of the two age groups in question. For the 7—10 age group, the most favorite flavor is chocolate, with 10,936 votes, and the least favorite is coffee, with 497 votes. The ratio is thus 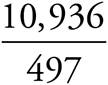= 22.0. For the 11—15 age group, the most favorite flavor is mint chocolate chip, with 9,495 votes, and the least favorite flavor is coffee, with 760 votes. The ratio is thus 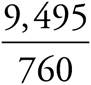= 12.5. To find out how many times greater the first ratio is, divide these numbers: 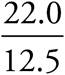= 1.8, which is (A).

Direct Variation

Direct variations or proportions occur when two variables increase together or decrease together. These questions generally ask you to make a conversion (such as from ounces to pounds) or to compare two sets of information and find a missing piece. For example, a proportion question may ask you to figure out the amount of time it will take to travel 300 miles at a rate of 50 miles per hour.

To solve proportion problems, just set up two equal fractions. One will have all the information you know, and the other will have a missing piece that you’re trying to figure out.

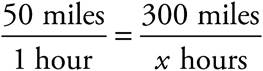
Be sure to label the parts of your proportion so you’ll know you have the right information in the right place; the same units should be in the numerator on both sides of the equals sign and the same units should be in the denominator on both sides of the equals sign. Notice how using a setup like this helps us keep track of the information we have and to find the information we’re looking for, so we can use Bite-Sized Pieces to work through the question.

Now we can cross-multiply and then solve for x: 50x = 300, so x = 6 hours.

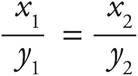
Let’s try the following question.

2.John receives $2.50 for every 4 pounds of berries he picks. How much money will he receive if he picks 90 pounds of berries?

A)$36.00

B)$42.25

C)$48.50

D)$56.25

Here’s How to Crack It

The question gives a relationship between two variables and asks for a value based on that relationship. To solve this, set up a proportion.

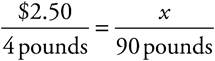
Now we can cross-multiply: 4x = 2.50 × 90, so 4x = 225, and x = 56.25. The answer is (D).

Occasionally, you may see a question that tells you there are two equal ratios. For example, if a question says that the ratio of 24 to 0.6 is equal to the ratio of 12 to y, you can solve for y by setting up a proportion. A proportion, after all, is really just two ratios set equal to each other.

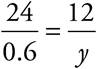
Then you can cross-multiply and solve to get 0.3 for your answer.

Inverse Variation

Inverse variation is simply the opposite of direct variation, or proportion. In a proportion, when one variable increases, the other variable also increases. With inverse variation, when one variable increases, the other variable decreases, or vice versa. These types of questions are generally clearly labeled and all you have to do is apply the inverse variation formula:

x₁y₁ = x₂y₂

Once you memorize the formula, applying it will become second nature to you.

Now try this one.

18.On a particular test, the percentage of people answering a question with the same response is inversely proportional to the number of the question. If 80% of test takers answered the 8th question correctly, then approximately what percentage of test takers gave the correct response to the 30th question?

A) 3%

B)13%

C)18%

D)21%

Here’s How to Crack It

The question asks for the percentage of test-takers that correctly answered the 30th question. The question tells us that the numbers are inversely proportional, so we need to figure out what to put into the formula. The first piece of information is that 80 percent of the people answered the 8th question correctly; we need to know the percent of people who answered the 30th question correctly. Let’s make x the percent and y the question number. Your equation should look like this:

(80)(8) = (x₂)(30)

When you solve the equation, you should end up with 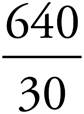or 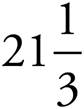, which is (D) (remember, when the question says “approximately,” you’ll probably have to round up or down).

Drill 3

Click here to download a PDF of Chapter 12 Drill 3.

Remember, answers to these drill questions can be found in Part IV!

a.If a student scores 70, 90, 95, and 105, what is the average (arithmetic mean) for these tests?

b.If a student has an average (arithmetic mean) score of 80 on 4 tests, what is the total of the scores received on those tests?

c.If a student has an average of 60 on tests, with a total of 360, how many tests has the student taken?

d.If the average of 2, 8, and x is 6, what is the value of x?

2, 3, 3, 4, 6, 8, 10, 12

e.What is the median of the group of numbers above?

f.What is the mode of the group of numbers above?

g.What is the range of the group of numbers above?

h.What percent of 5 is 6?

i.60 percent of 90 is the same as 50 percent of what number?

j.Jenny’s salary increased from $30,000 to $33,000. By what percent did her salary increase?

k.In 1980, factory X produced 18,600 pieces. In 1981, factory X produced only 16,000 pieces. By approximately what percent did production decrease from 1980 to 1981?

The amount of money in a savings account after m months is modeled by the function f(m) = 1,000(1.01)^m.

l.What was the original amount in the bank account?

m.By what percent does the amount in the account increase each month?

n.In a certain bag of marbles, the ratio of red marbles to green marbles is 7:5. If the bag contains 96 marbles, how many green marbles are in the bag?

o.One hogshead is equal to 64 gallons. How many hogsheads are equal to 96 gallons?

p.The pressure and volume of a gas are inversely related. If the gas is at 10 kPa at 2 liters, then what is the pressure when the gas is at 4 liters?

2.If 10 pecks are equivalent to 2.5 bushels, then 4 bushels are equivalent to how many pecks?

A) 4

B)10

C)12.5

D)16

Estimated Numbers of Cell Phone Users by Type (in millions)

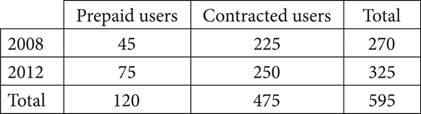
28.If a cell phone user is selected at random in 2008, what is the probability that user is a contracted user?

12.A forest fire is burning an area of forest that is 10 square miles. An air squad is able to reduce the size of the fire by 7% every 12 hours. If F(t) is the area being burned by the fire, which expression for F(t) represents the area of forest still on fire after t hours?

A)

B)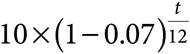

C)

D)

15.A student took five tests. He scored an average (arithmetic mean) of 80 on the first three tests and an average of 90 on the other two. Which of the following must be true?

I.The student scored more than 85 on at least one test.

II.The average (arithmetic mean) score for all five tests is less than 85.

III.The student scored less than 80 on at least two tests.

A)I only

B)II only

C)I and II

D)II and III

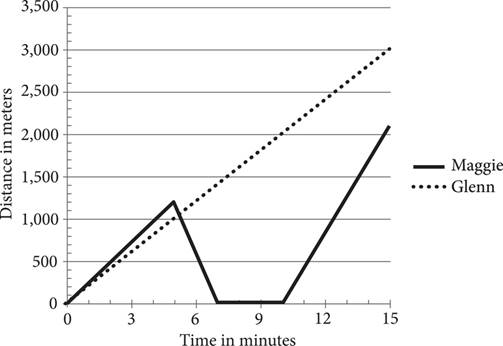
19.Maggie and Glenn both leave from the same house to go for a jog along a trail. Shortly after leaving, Maggie realizes she forgot her iPhone and returns home to find it before heading back out onto the same trail. The graph above shows how far each of them is from home for the first fifteen minutes of their jogs. Excluding the time she spends at home, which of the following is closest to Maggie’s average speed, in meters per second, during the portion of her jog shown?

A) 2.3

B) 5

C) 6.3

D)140

29.Marcia can type 18 pages per hour, and David can type 14 pages per hour. If they work together, how many minutes will it take them to type 24 pages?

22.In a political poll, 500 voters were first asked whether they were registered as Democrat, Republican, or Independent. The voters were then asked whether they planned to vote for Candidate A, for Candidate B, or were Undecided. The table below shows the results of the poll.

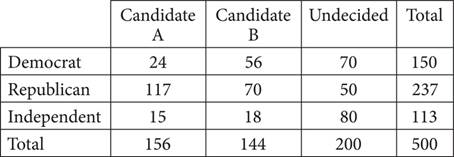
The number of registered Republicans who plan to vote for Candidate B is what percent greater than the number of registered Democrats who plan to vote for Candidate B?

A)14%

B)20%

C)25%

D)28%

25.The college that Everett attends in Chicago is exactly 200 miles from his parents’ home. When his parents come to visit him at school, they drive at an average speed of 45 miles per hour for maximum safety. When Everett drives home for winter break, his average speed is x% greater than the average speed at which his parents drive when they make the trip. Which of the following represents the time Everett saves on the 200-mile trip compared with his parents’ average time, in hours?

A)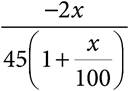

B)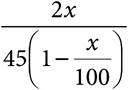

C)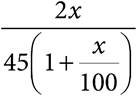

D)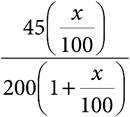

27.A survey company gathered data regarding people’s transportation habits in four major U.S. cities. The survey asked participants in each of these cities to indicate whether they regularly used a personal vehicle, public transportation, or neither to commute. Participants were not limited to one response and could check both personal vehicle and public transportation. The results are shown below.

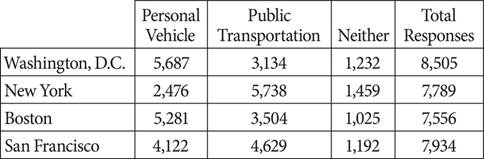
Which one of the following statements is supported by the data shown above?

A)Approximately 20% more people checked both personal vehicle and public transportation in Boston than in New York.

B)Washington, D.C. has the highest proportion of people that regularly use both public transportation and a personal vehicle.

C)The number of people that reported regularly using public transportation in New York is approximately 230% more than the number that reported regularly using a personal vehicle.

D)The ratio of personal vehicle use to public transportation use was lowest in San Francisco.

Summary

o The test is full of opportunities to use arithmetic instead of algebra—just look for your chances to use Plugging In and Plugging In the Answers (PITA).

o If a question has in terms of or variables in the answer choices, it’s a Plugging In question. Plug in your own number, do the math, find the target number, and use POE to get down to one correct answer.

o If a question doesn’t have variables but asks for a fraction or a percent of an unknown number, you can also plug in. Just substitute your own number for the unknown and take the rest of the question step by step.

o If a question has an unknown and asks for a specific amount, making you feel like you have to write an equation, try PITA instead.

o When a question asks about an average or arithmetic mean, use T = AN, plug in the values given in the question, and solve for what you need.

o The median is the middle value in a list of consecutive numbers. If there is an even number of elements, the median is the average of the two middle values.

o The mode is the most commonly occurring value in a list of numbers.

o The range is the difference between the greatest and least values in a list of numbers.

o Probability is a fractional value between 0 and 1 (inclusive), and it is equal to the number of outcomes the question is asking for divided by the total number of possible outcomes. It can also be expressed as a percent.

o Rates are closely related to averages. Use D = RT or W = RT just like you use T = AN. Remember that the PSAT likes to make you find the totals (distance or work in rate questions).

o Percent simply means “per 100.” Many percent questions can be tackled by translating English to math.

o Percent increase or decrease is .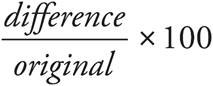

o Growth and decay are given by the formula final amount = original amount(1 ± rate)^{number of changes}.

o Set up ratios like fractions. Take care to put the first term of the ratio in the numerator and the second term in the denominator.

o Sometimes you’ll need to treat ratios like fractions or decimals. Use your calculator to turn the numbers into the easiest form to work the question.

o Direct variation or proportion means as one value goes up, the other goes up. The formula is .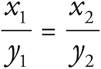

o Inverse variation means as one value goes up, the other goes down. The formula is x₁y₁ = x₂y₂.