PSAT/NMSQT Prep with Practice Tests - Princeton Review 2021

Advanced math
PSAT/NMSQT prep

There will be 14 questions on the PSAT that test what College Board calls “Passport to Advanced Math.” This category includes topics such as functions and quadratics. If you’ve learned these topics already in school, great! You’ll have a step up on the PSAT. If not, fear not—this chapter will give you the foundation needed for tackling these questions on the PSAT. You will also find information on how to tackle Meaning in Context questions and questions that determine the Analysis in Science score.

FUNCTIONS

In the Math Basics chapter, we looked at some concepts related to the xy-plane. Here, we will look at some more complicated topics involving functions and graphs. The functions on the PSAT mostly look like this:

f(x) = x² + 6x + 24

Just Follow the Instructions

Functions are like recipes. Each one is just a set of directions for you to follow. The College Board provides the ingredients and you work your magic.

Most questions of this type will give you a specific value to plug in for x and then ask you to find the value of the function. Each function is just a set of instructions that tells you what to do to x—or the number you plug in for x—in order to find the corresponding value for f(x) (a fancy name for y). Just plug your information into that equation and follow the instructions.

Let’s try an easy one.

2.If f(x) = x² + 3x − 3, what is the value of f(7)?

A)14

B)20

C)32

D)67

Here’s How to Crack It

The question asks for the value of f(7) given the definition of f(x). Function questions are just trying to see if you can follow the directions, so follow them! The instructions, in this case, are in the equation. So plug 7 into the equation and it should look like this: f(7) = (7)² + 3(7) − 3. Do the math and f(7) = 67. Therefore, the answer is (D).

Sometimes you’ll get more complicated questions. As long as you know that when you put in x, your function will spit out another number, you’ll be fine. Try this next one.

20.Let the function g be defined by g(x) = 5x + 2. If 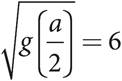, what is the value of a?

A)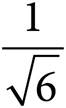

B)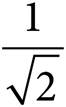

C)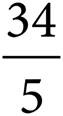

D)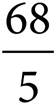

Here’s How to Crack It

The question asks for the value of a given the definition of g(x). This may look complicated, but just follow the directions. You know that g(x) = 5x + 2. You also know that 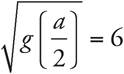. First, get rid of the square root by squaring both sides. Now you have 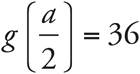. Usually there’s an x inside the parentheses. Treat this the same. This statement says that g of some number equals 36. We also know that g of some number is the same as 5x + 2. So 5x + 2 = 36. Simplify and you get . Careful, you’re not done. 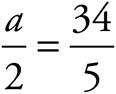You now know that , so 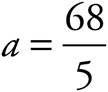, or (D).

Another way the PSAT can make functions more complicated is to give you two functions to deal with together. If you approach these questions one piece at a time, they will be easier to handle.

Here’s an example.

15.If f(x) = −x + and g(x) = x² − 7, what is the value of f(g(−2))?

Here’s How to Crack It

The question asks for the value of f(g(−2)) given the definitions of f(x) and g(x). With compound functions like this one, start from the inside and work your way out. Plug −2 into the g function to get g(−2) = (−2)² −7 = 4 − 7 = −3. Plug this value into the f function to get f(−3) = −(−3) + 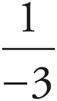= 3 − = 2. You can’t grid in mixed fractions, so convert it to an improper fraction or the decimal 2.66 or 2.67. Any of these would be acceptable answers.

Sometimes the PSAT will use a word problem to describe a function, and then ask you to “build a function” that describes that real-world situation.

Try one of those.

6.A scientist noted that the rate of growth of a tree which he had been observing is directly proportional to time. The scientist first measured the height of the tree to be 20 feet; two years later, the tree was 21 feet tall. If the tree continues to grow at a constant rate, which of the following represents the height of the tree in feet, y, as a function of time, x, in years since the scientist’s first measurement?

A)y(x) = 0.5x + 20

B)y(x) = 21x + 20

C)y(x) = x + 20

D)y(x) = 20x + 21

Here’s How to Crack It

The question asks for the function that represents the height of the tree over time. Instead of trying to write your own equation, use the ones in the answer choices. According to the question, 2 years after the first measurement, the tree was 21 feet tall. Therefore, when x = 2,y(x) = 21. Plug these points into the answers to see which answer works. Choice (A) becomes 21 = 0.5(2) + 20. Solve the right side of the equation to get 21 = 1 + 20, or 21 = 21. The correct answer is (A).

Roots of a Function

You may also be asked about the roots of a function. These are the solutions for x that you get when you solve the function or the places where the graph of the function crosses the x-axis. Here’s how this concept may be tested on the PSAT.

11.The graph of the function f in the xy-plane contains the points (−3, 0), (0, −2), and (4, 0). Which of the following is a factor of function f?

A)x − 2

B)x + 2

C)x + 3

D)x + 4

Here’s How to Crack It

The question asks for a factor of a function given points on the graph of the function. The factors are used to find the roots of a function, which are also known as the x-intercepts. At the x-intercept, y = 0. Therefore, the point (0, −2) is not a root, so that point cannot be used to determine the factors of the function. You can eliminate (A) and (B) because they include 2. According to the question, one of the x-intercepts is at (−3, 0). This means that one solution to the function can be found by x + 3 = 0, and one of the factors of the function is x + 3. The other factor would be (x − 4), but that’s not a choice. The correct answer is (C).

Drill 1

Click here to download a PDF of Chapter 13 Drill 1.

Answers can be found in Part IV.

3.Which of the following equivalent forms of the equation x² + 8x + 15 = 0 would be the most useful for finding the x-intercepts of the equation?

A)x(x) + 8(x) + 15 = 0

B)x² + 3x + 5x + 15 = 0

C)(x + 3)(x + 5) = 0

D)x² + 8x + 4 + 11 = 0

4.Monster Truck Inc. leases a new truck for a down payment of $3,200 plus monthly payments of $380 per month for 36 months. Which of the following functions, f, represents the total amount paid, in dollars, after m months, where 0 ≤ m ≤ 36?

A)f(m) = 380 + 3,200m

B)f(m) = 3,200 + 36m

C)f(m) = 3,200 + 380m

D)f(m) = 10,480 − 380m

15.If f(x) = x² − x + 4, a is non-negative, and f(a) = 10, what is the value of a?

9.The number of bonus points, B(p), that a credit card holder receives is given by the function B(p) = ap + 7, where p represents the number of purchases made and a is a constant. If the number of purchases is increased by 4, the number of bonus points increases by 25. What is the value of a?

A) 4

B) 4.5

C) 6.25

D)11

21.If f(x) = 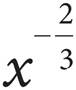, what is the value of ?

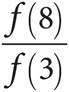A)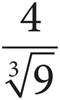

B)

C)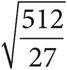

D)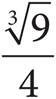

23.The temperature, T, in degrees Celsius on a winter day can be written as a function of x, the time in hours since midnight (12:00 A.M.), as shown below.

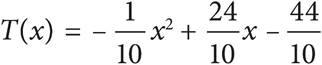
If 100 = x² − 24x + 144 is an equivalent form of the equation when T(x) = 0, which of the following gives a time on that day when the temperature was 0°C?

A) 6 P.M.

B)10 P.M.

C) 3 A.M.

D) 9 A.M.

12.The table above shows selected values for the linear function f(x). What is the value of j?

A)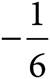

B)

C)

D)

Questions 30 and 31 refer to the following information.

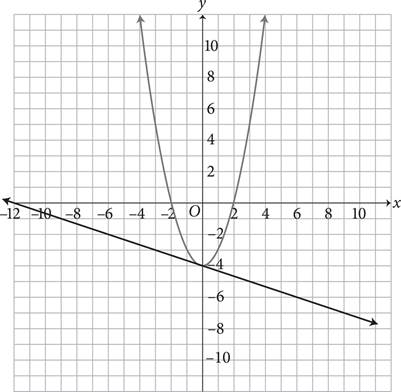
In the above graph, parabola f(x) is represented by the equation f(x) = x² − 4 and line g(x) is represented by the equation g(x)= −x −4. Line g(x) intersects parabola f(x) at point (0, −4).

30.For x = 12, how much greater is the value of f(x) than g(x)?

31.A new line, h(x), is added to the graph. The line h(x) is perpendicular to line g(x), intersecting with line g(x) at the point (−12, 0). What is the x-coordinate of the point where line h(x) will intersect parabola f(x) in Quadrant 1?

QUADRATIC EQUATIONS

Ah, quadratics. You’re likely to see several questions on the PSAT that require you to expand, factor, or solve quadratics. You may even need to find the vertex of a parabola or the points of intersection of a quadratic and a line. So let’s review, starting with the basics.

Expanding

Most often you’ll be asked to expand an expression simply by multiplying it out. When working with an expression of the form (x + 3)(x + 4), multiply it out using the following rule:

FOIL = First Outer Inner Last

Start with the first figure in each set of parentheses: x × x = x².

Now do the two outer figures: x × 4 = 4x.

Next, the two inner figures: 3 × x = 3x.

Finally, the last figure in each set of parentheses: 3 × 4 = 12.

Add them all together, and we get x² + 4x + 3x + 12, or x² + 7x + 12.

Factoring

If you ever see an expression of the form x² + 7x + 12 on the PSAT, there is a good chance that factoring it will be the key to cracking it.

The key to factoring is figuring out what pair of numbers will multiply to give you the constant term (12, in this case) and add up to the coefficient of the x term (7, in this question).

Let’s try an example:

x² + 7x + 12

Step 1: Draw two sets of parentheses next to each other and fill an x into the left side of each. That’s what gives us our x² term.

(x )(x )

Step 2: 12 can be factored a number of ways: 1 × 12, 2 × 6, or 3 × 4. Which of these adds up to 7? 3 and 4, so place a 3 on the right side of one parenthesis and a 4 in the other.

(x 3)(x 4)

Step 3: Now we need to figure out what the correct signs should be. They should both be positive in this case, because that will sum to 7 and multiply to 12, so fill plus signs into each parenthesis.

(x + 3)(x + 4)

If you want to double-check your work, try expanding out (x + 3)(x + 4) using FOIL and you’ll get the original expression.

Now try the following question.

8.Travis determines that the average speed of his kayak traveling down the river when he is not paddling can be calculated using the formula 4r² − 40r + 100, where r represents the strength of the river’s current in feet per second. Which of the following expressions would be an equivalent formula that Travis could use to determine his kayak’s speed?

A)(2r + 10)²

B)(2r + 10)(2r − 10)

C)4(r + 5)²

D)4(r + 5)²

Here’s How to Crack It

The question asks for an equivalent formula that can be used to determine Travis’s speed. To compare the equation in the question with the answer choices, you need to either factor the equation in the question or expand out the answer choices. The first option is probably faster. Start by factoring a 4 out of the entire equation to get 4(r² − 10r + 25). Now, determine what two numbers can be added to get −10 and multiplied to get 25. In this case, it’s −5 and −5. The equation becomes 4(r − 5)(r − 5) or 4(r − 5)², which is (D).

Don’t forget that you can also plug in on a question like the last one. Let’s look at one in which Plugging In makes a strange question much more manageable.

8.If the expression x + 2(x − 4) is multiplied by R to form the expression 3x² − 5x − 8, then which of the following is equivalent to R?

A)x + 1

B)x + 2

C)x + 3

D)x + 4

Here’s How to Crack It

The question asks for an expression that is equivalent to R. Whenever the question and the answers include variables, see if you can plug in. If x = 2, the first expression becomes 2 + 2(2 − 4) = 2 + 2(−2) = 2 + (−4) = −2, and the second expression becomes 3(2²) − 5(2) − 8 = 3(4) −10 − 8 = 12 − 10 − 8 = −6. To find R, set up the following equation: −2R = −6. Solve for R to get R = 3. Plug 2 in for x in the equations to see which answer equals the target number of 3. Choice (A) becomes 2 + 1 = 3. Keep (A), but check the remaining answers just in case. Choice (B) becomes 2 + 2 = 4, (C) becomes 2 + 3 = 5, and (D) becomes 2 + 4 = 6. Eliminate (B), (C), and (D). The correct answer is (A).

Solving Quadratic Equations

Sometimes you’ll want to factor to solve an equation. In this case, there will be two possible values for x, called the roots of the equation. To solve for x, use the following steps:

Step 1: Make sure that the equation is set equal to zero.

Step 2: Factor the equation.

Step 3: Set each parenthetical expression equal to zero. So if you have (x + 2)(x − 7) = 0, you get (x + 2) = 0 and (x − 7) = 0. When you solve for each, you get x = −2 and x = 7. Therefore, −2 and 7 are the solutions or roots of the equation.

Try the following question.

4.If b² + 2b − 8 = 0, and b < 0, what is the value of b?

A)−6

B)−4

C)−2

D) 0

Here’s How to Crack It

The question asks for the value of b in a quadratic equation. Begin by using Process of Elimination. Since the question states that b < 0, eliminate (D). Now follow the steps:

1.  The equation is already set equal to zero.

2.  You can now factor the left side of the equation to get (b + 4)(b − 2) = 0.

3.  When you set each parenthetical expression equal to zero, you get b = −4 and b = 2. Since b < 0, the answer is (B).

An alternative approach to this question is to plug in the answers. For (A), plug b = −6 into the equation to get (−6)² + 2(−6) − 8 = 0. Solve the left side of the equation to get 36 − 12 − 8 = 0, or 16 = 0. Since this statement is not true, eliminate (A). For (B), plug b = − 4 into the equation to get (−4)² + 2(−4) − 8 = 0. Solve the left side of the equation to get 16 − 8 − 8 = 0, or 0 = 0. Since this statement is true, the correct answer is (B).

Sometimes, solving will get a little trickier. When quadratics do not factor easily and there are no answer choices to plug in, you can use the quadratic formula to solve.

The values of x for a quadratic equation in the form y = ax² + bx + c are

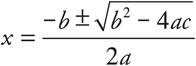
Let’s try one.

29.If y = x² − 4x + 3.75, what is one possible value of x?

Here’s How to Crack It

The question asks for the value of x in a quadratic equation. This one is not easy to factor, so try the quadratic formula. In the given equation, a = 1, b = −4, and c = 3.75. Therefore,

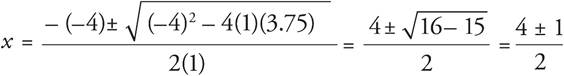
So x equals (or 2.5) and (or 1.5). Any of these 4 options could be entered into the grid.

You may have noticed that this is a calculator question. Another option for this one would be to graph the equation on your calculator to determine the x-intercepts, which are the roots, or solutions, to the equation.

Other Quadratic Questions

Sometimes, quadratic equations will be tested with word problems or charts. Let’s look at these types of questions.

29.An Olympic shot-putter throws a heavy spherical object that follows a parabolic trajectory. The equation describing the trajectory of the shot-putter’s throw is y = −0.04x² + 2.02x + 5.5, where y represents the height of the object in feet and x represents the horizontal distance in feet traveled by the object. What is the original height of the object (in feet) immediately before it leaves the shot-putter’s hand?

Here’s How to Crack It

The question asks for the original height of an object based on an equation for the object’s trajectory. According to the question, x represents the horizontal distance in feet traveled by the object, and y represents the height. Before the shot-putter throws the object, x = 0. Plug 0 into the equation and solve for y. The equation becomes y = −0.04(0²) + 2.02(0) + 5.5 = 0 + 0 + 5.5 = 5.5. The correct answer is 5.5.

Now look at an example of a chart-based quadratic question.

Trajectory of a Dolphin’s Jump

14.The table above shows the horizontal distance and vertical height, both in feet, of a typical dolphin jumping out of the water (a height of 0 represents the surface of the water). If d represents the horizontal distance and h represents the vertical height, which of the following equations would best represent the trajectory of the dolphin’s jump?

A)h = −03d² + 3d

B)h = −0.4d² + 4d

C)h = −0.5d² + 5d

D)h = −0.6d² + 6d

Here’s How to Crack It

The question asks for an equation to model the trajectory of a dolphin’s jump based on a table of values. This is a similar task to “building a function” that we discussed earlier in this chapter. You should plug values from the table into the equations in the answer choices to see which equation works. According to the table, when d = 1, h = 2.7. Plug these values into (A) to get 2.7 = −0.3(1²) + 3(1). Solve the right side of the equation to get 2.7 = −0.3 + 3 or 2.7 = 2.7. Keep (A), but check the remaining answers just in case. Choice (B) becomes 2.7 = −0.4(1²) + 4(1). Solve the right side of the equation to get 2.7 = −0.4 + 4 or 2.7 = 3.6. This is not true, so eliminate (B). Choice (C) becomes 2.7 = −0.5(1²) + 5(1). Solve the right side of the equation to get 2.7 = −0.5 + 5 or 2.7 = 4.5. Eliminate (C). Choice (D) becomes 2.7 = −0.6(1²) + 6(1). Solve the right side of the equation to get 2.7 = −0.6 + 6 or 2.7 = 5.4. Eliminate (D). The correct answer is (A).

Forms of Quadratics

When graphed in the xy-plane, quadratics form a parabola. The PSAT will ask questions using three different forms of the equation for a parabola.

The standard form of a parabola equation is as follows:

y = ax² + bx + c

In the standard form of a parabola, the value of a tells whether a parabola opens upwards or downwards (if a is positive, the parabola opens upwards, and if a is negative, the parabola opens downwards).

The factored form of a parabola equation is as follows:

y = a(x − s)(x − t)

In the factored form, s and t are the x-intercepts.

We discussed factoring quadratics a few pages back. The result of factoring a parabolic equation is the factored form.

The vertex form of a parabola equation is as follows:

y = a(x − h)² + k

In the vertex form, the point (h, k) is the vertex of the parabola.

Simply knowing what the vertex form looks like may help you answer a question, like the following example.

6.Which of the following equations has its vertex at (−4, 3)?

A)y = (x − 4)² + 3

B)y = (x + 4)² + 3

C)y = (x − 3)² + 4

D)y = (x + 3)² − 4

Here’s How to Crack It

The question asks for a quadratic equation that has a given vertex. If you know the vertex form, you can create the correct equation for the parabola. Be careful with the signs, though, as the signs are all changing in the answer choices. In the vertex (−4, 3), −4 is h and 3 is k. The correct answer should end in + 3, so eliminate (C) and (D). For the (x − h)² part of the equation, it becomes (x − (−4))², or (x + 4)², so the correct answer is (B).

Knowing the form makes Process of Elimination a quick way to answer these, but if you forget the form, you can always plug in the given point to see which equation is true.

The vertex form is great for answering questions about the minimum or maximum value a parabolic function will reach or the x-value that results in that minimum or maximum y-value. So another good thing to know is the method for turning a quadratic in the standard form into the vertex form. Here are the steps to do that.

To convert a parabola equation in the standard form to the vertex form, complete the square.

1. Make y = 0, and move any constants over to the left side of the equation.

2. Take half of the coefficient on the x-term, square it, and add it to both sides of the equation.

3. Convert the x-terms and the number on the right to square form: (x − h)².

4. Move the constant on the left back over to the right and set it equal to y again.

Say you were given the equation y = x² − 4x − 12. You would make it 0 = x² − 4x − 12, and then 12 = x² − 4x. You’d add 4 to both sides to get 16 = x² − 4x + 4, and then convert the right side to the square form to get 16 = (x − 2)². Finally, you’d move the 16 back over and set it equal to y to get y = (x − 2)² − 16.

Drill 2

Click here to download a PDF of Chapter 13 Drill 2.

Answers can be found in Part IV.

3.In his physics class, Yigit determined that the height in feet (h) of a projectile t seconds after being launched can be expressed using the function h(t) = −5t² + 20t + 45. Which of the following values of t would be most helpful in finding the initial height of the projectile?

A)t = 0

B)t = 1

C)t = 2

D)t = 3

4.If 12 − (t + 2)² = 3, which of the following could be the value of t?

A)−9

B)−5

C) 5

D) 7

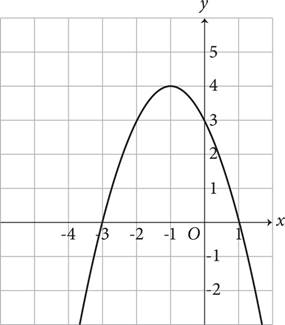
6.Which of the following equations is shown in the graph above?

A)y = −(x − 3)(x + 1)

B)y = −(x + 3)(x − 1)

C)y = −(x + 3)(x + 4)

D)y = −(x − 1)(x + 4)

9.Aubri determines that her score in a particular video game can be calculated using the formula x⁴ − y⁴, where x represents the number of treasures she discovers, and y represents the number of hidden traps she falls into. Which of the following expressions would be a suitable equivalent for Aubri’s score calculation formula?

A)(x + y) (x − y) (x² + y²)

B)(x + y)²(x² + y²)

C)(x − y)²(x² + y²)

D)(x + y)(x − y)(x² − y²)

10.Which of the following equations has a vertex of (−5, 2)?

A)y = (x + 5)² − 2

B)y = (x −5)² − 2

C)y = 2(x + 5)² + 2

D)y = 2(x − 5)² + 2

14.The profit that a donut shop makes can be expressed by the equation P = −4(x − 3)² + 2,000, where x is the price per donut sold (in dollars). What price, in dollars, should the donut shop charge its customers in order to maximize its profit?

23.In the equation x² + 24x + c = (x + 9)(x + p), c and p are constants. If the equation is true for all values of x, what is the value of c?

A) 33

B)135

C)144

D)216

26.The stream of water that shoots out of a public fountain in Central Park takes the form of a parabola. The water shoots from a spout that is 8 feet above the ground and reaches a maximum height of 39.25 feet. If y represents the height of the water and x represents the time (in seconds), which of the following equations could describe the trajectory of the stream of water?

A)y = −x² + 15

B)y = −5x² + 25x + 8

C)y = 2x² + 32x + 8

D)y = 8x + 39.25

ANALYSIS IN SCIENCE

If some of the questions you’ve seen so far are reminding you of science class, you’re not crazy. One of the cross-test scores the PSAT aims to measure is called Analysis in Science. This means that questions on science-based ideas will show up in Reading and Writing passages and also in Math questions.

One way this concept will be tested is through word problems. Many of the strategies we’ve already discussed, such as translating or Plugging In, will help you to answer these questions, regardless of the scientific context.

Here’s an example.

29.The electric potential of a point charge Q is given by the equation 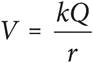, where V is the charge in volts or Joules per Coulomb, Q is the charge in Coulombs, r is the distance from the charge in meters, and k is a constant equal to 9.0 × 10⁹ Nm²/C². If a point charge has an electric potential of 225 volts at a distance of 1 meter from the charge, what is the charge in nanocoulombs? (Note: 1 Coulomb = 10⁹ nanocoulombs.)

Here’s How to Crack It

The question asks for the charge in nanocoulombs for a given electric potential and distance. Start by identifying the values of all of the variables given. According to the question, r = 1, k = 9.0 × 10⁹, and V = 225 coulombs. The question asks for the charge in nanocoulombs, so multiply 225 by 10⁹ and you find that V = 225 × 10⁹. Plug these values into the equation to get 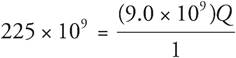. Solve for Q by dividing both sides by 9.0 × 10⁹ to get 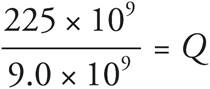, or 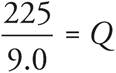. So 25 = Q, and that’s your answer.

Sometimes, you will be asked science questions based on a chart or graph. In those cases, carefully look up the numbers in question, do the required calculations, and eliminate answers that aren’t true.

Let’s look at one.

Marble Ramp Rolling Times

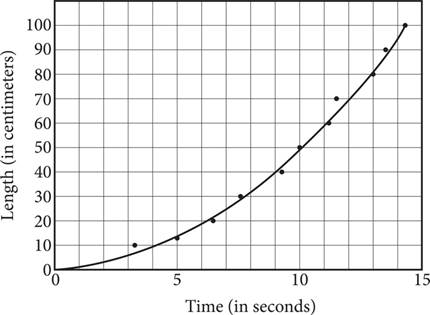
4.A student is rolling a marble down ramps of varying lengths. The scatterplot above shows the time, in seconds, it takes the marble to roll down each ramp. Based on the curve of best fit to the data represented, which of the following is the closest to the expected length of a ramp if a marble takes 12 seconds to roll down?

A)61

B)72

C)79

D)84

Here’s How to Crack It

The question asks for the expected length of a ramp given a certain roll time based on the graph. Roll time is shown on the horizontal axis of the graph, given in seconds. Look for the mark indicating 12 seconds on this axis; then draw a vertical line from that mark to the curve of best fit. Once you hit it, draw a horizontal line over to the vertical axis. It should hit between 60 and 80 centimeters, right around 70. This makes (B) the credited response, since it is slightly closer to the mark for 70. Draw your lines carefully, using your answer sheet as a straightedge if necessary, since three of these answer choices are between 60 and 80.

You may also be asked to graph the data presented in a table. Your knowledge of graphing in the xy-plane should help you with most of those. If anything gets too tricky, consider skipping it and spending your time on something else.

The last science-based question type you may see doesn’t involve charts, graphs, or equations. In fact, these don’t even look much like math questions at all. They will have a lot of words to describe a scientific situation and ask about the conclusion that can be drawn. Just use a lot of Process of Elimination and a little knowledge of what makes a good experiment, and you should be fine.

Try this one.

15.A psychologist wants to know whether there is a relationship between increased water consumption and exam scores. He obtains survey responses from a random sample of 3,500 20-year-old college students in the United States and finds a strong positive correlation between increased water consumption and test scores. Which of the following conclusions is well-supported by the data?

A)There is a positive association between increased water consumption and test scores for 20-year-olds in the United States.

B)There is a positive association between increased water consumption and test scores for adults in the United States.

C)High test scores are caused by increased water consumption for 20-year-olds in the United States.

D)High test scores are caused by increased water consumption for adults in the United States.

Here’s How to Crack It

The question asks for the conclusion that is well-supported by the data of a survey. Consider each answer choice one at a time and use Process of Elimination. Choice (A) merely restates what the evidence says, which makes it a safe conclusion, so keep it. Choice (B) is similar but shifts from “20-year-old college students” to “adults.” This is a less safe conclusion than (A), because it generalizes from a more particular group, so eliminate (B). Choices (C) and (D) both introduce the idea of causation. This is a problem—no information was given about cause. Maybe people who tend to score higher on tests are also smart enough to drink more water, or maybe there is another factor causing both high test scores and increased water consumption. Eliminate (C) and (D) and choose (A).

MEANING IN CONTEXT

Some questions, instead of asking you to come up with an equation, just want you to recognize what a part of the equation stands for. It sounds like a simple enough task, but when you look at the equation, they have made it really hard to see what is going on. For this reason, Meaning in Context questions are a great opportunity to plug in real numbers and start to see how the equation really works!

First things first, though, you want to think about your POOD. Does this question fit into your pacing goals? It might take a bit of legwork to get an answer, and you may need that time to go collect points on easier, quicker questions.

If this question does fit into your pacing plan, you should read carefully, label everything you can in the equation, and POE to get rid of any answer choices that are clearly on the wrong track. Then, it’s time to plug some of your own numbers in to see what is going on in there.

Here’s an example.

n = 1,273 − 4p

7.The equation above was used by the cafeteria in a large public high school to model the relationship between the number of slices of pizza, n, sold daily and the price of a slice of pizza, p, in dollars. What does the number 4 represent in this equation?

A)For every $4 the price of pizza decreases, the cafeteria sells 1 more slice of pizza.

B)For every dollar the price of pizza decreases, the cafeteria sells 4 more slices of pizza.

C)For every $4 the price of pizza increases, the cafeteria sells 1 more slice of pizza.

D)For every dollar the price of pizza increases, the cafeteria sells 4 more slices of pizza.

Here’s How to Crack It

The question asks what the number 4 represents in an equation modeling a certain situation. First, read the question very carefully, and use your pencil to label the variables. You know that p is the price of pizza, and n is the number of slices, so you can add that information to the equation. If you can, eliminate answer choices that don’t make sense. But what if you can’t eliminate anything, or you can eliminate only an answer choice or two?

Even with everything labeled, this equation is difficult to decode, so it’s time to plug in! Try a few of your own numbers in the equation, and you will get a much better understanding of what is happening.

Let’s try it out with p = 2. When you put 2 in for p, n = 1,273 − 4(2) or 1,265.

So, when p = 2, n = 1,265. In other words, at $2 a slice, the cafeteria sells 1,265 slices.

When p = 3, n = 1,261, so at $3 a slice, the cafeteria sells 1,261 slices.

When p = 4, n = 1,257, so at $4 a slice, the cafeteria sells 1,257 slices.

So now, let’s use POE. First of all, is the cafeteria selling more pizza as the price goes up? No, as the price of pizza goes up, the cafeteria sells fewer slices of pizza. That means you can eliminate (C) and (D).

Choice (A) says that for every $4 the price goes down, the cafeteria sells 1 more slice of pizza. Does your plugging in back that up? No. The cafeteria sells 8 more slices of pizza when the price drops from $4 to $2, so (A) is no good.

Now, let’s take a look at (B). Does the cafeteria sell 4 more slices of pizza for every dollar the price drops? Yes! Choice (B) is the correct answer.

Here are the steps for using Plugging In to solve Meaning in Context questions:

Meaning In Context

1. Read the question carefully. Make sure you know which part of the equation you are being asked to identify.

2. Use your pencil to label the parts of the equation you can identify.

3. Eliminate any answer choices that clearly describe the wrong part of the equation, or go against what you have labeled.

4. Plug in! Use your own numbers to start seeing what is happening in the equation.

5. Use POE again, using the information you learned from plugging in real numbers, until you can get it down to one answer choice. Or, get it down to as few choices as you can, and guess.

Let’s look at a slightly different one now.

7x + y = 133

10.Jeffrey has set a monthly budget for purchasing frozen blended mocha drinks from his local SpendBucks coffee shop. The equation above can be used to model the amount of his budget, y, in dollars, that remains after buying coffee for x days in a month. What does it mean that (19, 0) is a solution to this equation?

A)Jeffrey starts the month with a budget of $19.

B)Jeffrey spends $19 on coffee every day.

C)It takes 19 days for Jeffrey to drink 133 cups of coffee.

D)It takes 19 days for Jeffrey to run out of money in his budget for purchasing coffee.

Here’s How to Crack It

The question asks for the meaning of a given solution to an equation modeling a situation. Start by labeling the x and the y in the equation to keep track of what they stand for. Use your pencil to write “days” above the x and “budget” above the y. So 7 × days + budget = 133. Hmm, still not very clear, is it? One way to approach this is to plug in the point (19, 0). If x = days = 19 when y = budget = 0, then Jeffrey will have no budget left after 19 days. This matches (D).

If you have trouble seeing this, you can use the answer choices to help you plug in. If (A) is true, the budget at the start of the month, when days = 0, is $19. Plug these values into the equation to see if it is true. Is 7 × 0 + 19 = 133? Not at all, so eliminate (A). If (B) is true, Jeffrey drinks a lot of coffee! Let’s try some numbers and see if it works. For x = 1, the equation becomes 7(1) + y = 133 or y = 126, and for x = 2, it is 7(2) + y = 133 or y = 119. The difference in y, the budget remaining, is 126 − 119 = 7, so that’s not $19 per day. Eliminate (B), so only (C) and (D) remain. These both have 19 for the number of days, and the point (19, 0) would indicate that 19 is the x value, or days. If you saw that right away—great! That would allow you to skip right to testing (C) and (D).

For (C), you can plug in 19 for days in the equation to get 7 × 19 + budget = 133, or budget = 0. Does that tell you how many cups of coffee Jeffrey drank? You have no information about the cost of a single cup of coffee, so the answer can’t be (C). It does tell you, however, that after 19 days, Jeffrey has no budget left, so (D) is not only the one remaining answer, but it is also the correct one!

Drill 3

Click here to download a PDF of Chapter 13 Drill 3.

Answers can be found in Part IV.

3.An oceanographer is trying to determine the concentration profile of dissolved oxygen in the ocean at depths lower than 10 meters. He determines that the dissolved oxygen concentration is 0.0022 g/L at a depth of 15 meters, and it is 0.00125 g/L at a depth of 20 meters. If C(d) is the concentration of dissolved oxygen at d meters, which of the follow equations best describes the profile below 10 meters?

A)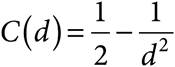

B)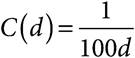

C)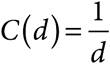

D)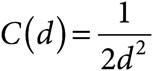

6.A shipping company pays a driver a fixed fee for each delivery, and deducts a separate fee daily for the use of the company’s delivery truck. The driver’s net pay in dollars, P, for one day is given by the equation P = 8d − 40, where d is the number of deliveries made in one day. What does the number 40 most likely represent?

A)The amount, in dollars, that the company deducts for use of the delivery truck

B)The amount, in dollars, that the driver is paid for each delivery

C)The average number of deliveries per hour made by the driver

D)The total number of deliveries made per day by the driver

9.At a buffet restaurant, students pay $5 per meal and non-students pay $7. The total revenue, R, in dollars, earned per day by the restaurant is given by the equation R = 5s + 7n, where s is the number of student customers and n is the number of non-student customers. Which of the following represents the total number of customers on a given day?

A)s − n

B)s + n

C)sn

D)

T(t) = ΔT^(−kt)

7.The simple cooling of an object can be represented by the equation above, where T is temperature in degrees Celsius, k is a rate constant, and t is time. What might the quantity ΔT represent?

A)Temperature at a certain time

B)The difference between the initial temperature of the object and the temperature of its surroundings

C)A conversion from Celsius to Fahrenheit

D)A constant factor that is dependent on the object

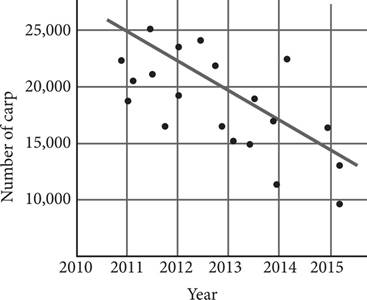
10.Between 2010 and 2015, researchers tracked populations of Crucian carp in the Ohio River. The graph above displays population sizes as counted by the researchers. According to the line of best fit, what is the approximate average yearly decrease in the number of Crucian carp?

A) 1

B) 2.5

C)1,200

D)2,500

8.A group of students decided to have a car wash to raise funds for the school. The students charged the same rate to wash each car, and they paid for cleaning supplies out of the proceeds. If the net amount, N(c), in dollars, raised from washing c cars is given by the function N(c) = 8c − 0.40c, which of the following can be deduced from the function?

A)The students paid a total of $8 for cleaning supplies.

B)The students paid a total of $40 for cleaning supplies.

C)The students paid $0.40 per car for cleaning supplies.

D)The students paid $8 per car for cleaning supplies.

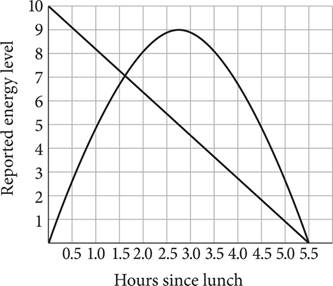
12.Two employees at a certain company were asked to gauge their energy levels on a scale of 1 to 10 after eating lunch at noon. The results were averaged and plotted as illustrated in the above figure. Which of the following statements is most consistent with the given data?

A)Both employees experienced the same fluctuation in energy during the afternoon hours.

B)Both employees were drowsy after eating big lunches.

C)One of the employees consumed energy-boosting foods and drinks and became less energetic throughout the afternoon.

D)One of the employees consumed foods that resulted in her feeling more energetic throughout the day.

11.Delphine is studying the growth of bacteria in a petri dish. She grows 100 colonies of bacteria in dishes at varying temperatures to find the optimal temperature for bacteria growth. The temperature of the 10 colonies with the most rapid growth is used to determine the optimal temperature range, which Delphine finds to be from 30° to 37°C, inclusive. Which of the following inequalities represents the optimal temperature range, t, for bacteria growth?

A)|t + 7|≤ 37

B)|t − 3.5| ≤ 33.5

C)|t − 30|≤ 7

D)|t − 33.5| ≤ 3.5

13.The sum, S, of a set of n consecutive integers is given by the equation S = 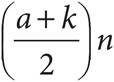. What does a + k represent?

A)The sum of the two least integers

B)The sum of the least and greatest integers

C)The sum of the two middle integers

D)The sum of the two greatest integers

23.If interest deposits are made monthly into an account with a beginning balance of $250, supposing no withdrawals are made from the account, the balance B of an account with an annual interest rate of 5% after t years can be computed using the equation below.

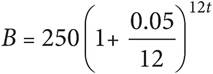
Which of the following describes what the quantity 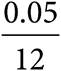represents in the equation?

A)The amount of money deposited into an account with balance B during a given month

B)The amount of money in an account with balance B after a monthly interest deposit is made

C)The percentage of the starting balance B added during a monthly interest deposit

D)The number of months over which interest payments will be made in a year

Summary

o Given a function, you put an x value in and get an f(x) or y value out.

o Look for ways to use Plugging In and PITA on function questions.

o For questions about the graphs of functions, remember that f(x) = y.

o If the graph contains a labeled point or the question gives you a point, plug it into the equations in the answers and eliminate any that aren’t true.

o To find a point of intersection, set the equations equal, plug a given point into both equations to see if it works, or graph the equations on your calculator when it is allowed.

o When solving quadratic equations, you may need to FOIL or factor to get the equation into the easiest form for the question task.

o The standard form of a quadratic equation is ax² + bx + c = 0. The factored form is y = a(x − s)(x − t), where s and t are the x-intercepts.

o To solve for the roots of a quadratic equation, set it equal to zero by moving all the terms to the left side of the equation, or use the quadratic formula:

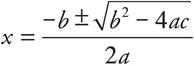
o The vertex form of a parabola equation is y = a(x − h)² + k, where (h, k) is the vertex. To get a parabola in the standard form into vertex form, complete the square.

o Plugging In can also be used on Meaning In Context questions. If a question asks you to identify a part of an equation, plug your own amounts into the equation so you can start to see what is going on.

o Analysis in Science questions may seem weird, but they can usually be handled with the same strategies as those used for other math questions. Plug in or translate, read the chart or text carefully, and always use Process of Elimination to get rid of answers that don’t match the data or don’t make sense.

o If you come across a hard Meaning in Context question or Science question, see if you can eliminate anything and make a guess. If not, find another question to do!