Additional math topics - PSAT/NMSQT prep

PSAT/NMSQT Prep with Practice Tests - Princeton Review 2021

Additional math topics
PSAT/NMSQT prep

The PSAT has a clever name for the rest of the math concepts tested—Additional Topics. Well, maybe it’s not that clever. It consists of some geometry concepts and possibly a question about imaginary numbers. While there are many geometry ideas that could be tested, these Additional Topics will really make up only a small fraction of the PSAT. Spend time on this chapter only after you have mastered the topics and techniques in the previous three chapters.

GEOMETRY

Lines and Angles

Common sense might tell you what a line is, but for this test you are going to have to learn the particulars of a line, a ray, and a line segment.

A line continues on in each direction forever. You need only two points to form a line, but that line does not end at those points. A straight line has 180 degrees on each side.

A ray is a line with one distinct endpoint. Again, you need only two points to designate a ray, but one of those points is where it stops—it continues on forever in the other direction. A ray has 180 degrees as well.

A line segment is a line with two distinct endpoints. It requires two points, and it is the length from one point to the other. A line segment has 180 degrees.

Whenever you have angles on a line, remember the rule of 180: The angles on any line must add up to 180. These angles are called supplementary angles. In the figure below, what is the value of x? We know that 2x + x must add up to 180, so we know that 3x = 180. This makes x = 60.

Note: Figure not drawn to scale.

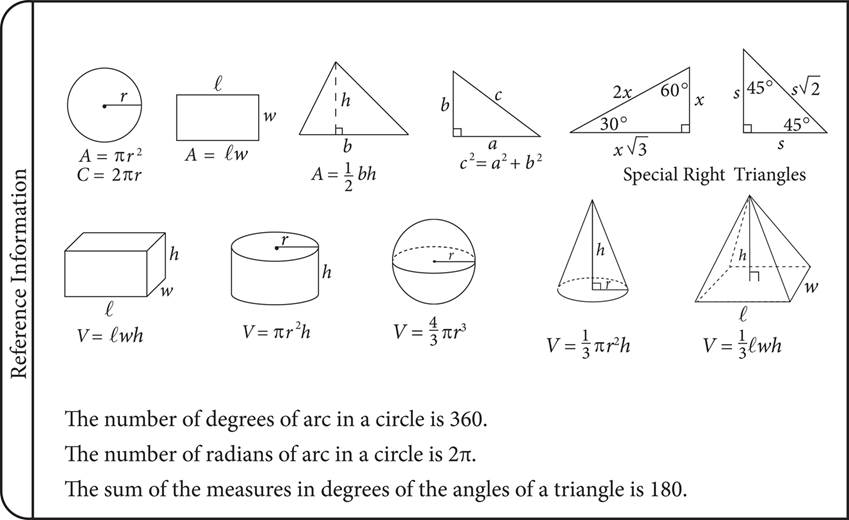
If two lines cross each other, they make vertical angles—that is, angles opposite each other when two lines intersect. These angles will always have the same measure. In the figure below, z and x are vertical angles, and y and the 130° angle are vertical angles. Also, we know that z must equal 50, since 130 + z must equal 180. We know that y is 130, since it is across from the angle 130. We also know that x is 50, since it is across from z.

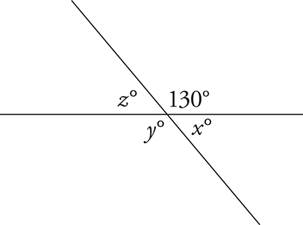
Any time you have two parallel lines and a line that crosses them, you have two kinds of angles: big angles and small angles. All of the big angles have the same measure, and all of the small angles have the same measure. In the following figure, angles a, d, e, and h all have the same measure; angles b, c, f, and g also all have the same measure. The sum of the measure of any big angle plus any small angle equals 180 degrees.

Four-Sided Figures

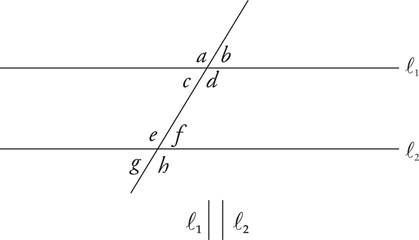
A figure with two sets of parallel sides is a parallelogram. In a parallelogram, the opposite angles are equal, and any adjacent angles add up to 180 degrees. (In the left-hand figure above, x + y = 180 degrees.) Opposite sides are also equal. The sum of all angles of a parallelogram is 360 degrees.

If all of the angles are also right angles, then the figure is a rectangle. And if all of the sides are the same length, then the figure is a square.

The area of a square, rectangle, or parallelogram is length × width. (In the parallelogram above, the length is shown by the dotted line.)

The perimeter of any figure is the sum of the lengths of its sides. A trapezoid with sides of 6, 8, 10, and 8 has a perimeter of 32.

Thinking Inside the Box

Here’s a progression of quadrilaterals from least specific to most specific:

quadrilateral = 4-sided figure

parallelogram = a quadrilateral in which opposite sides are parallel

rectangle = a parallelogram in which all angles equal 90°

square = a rectangle in which all angles and all sides are equal

Drill 1

Click here to download a PDF of Chapter 14 Drill 1.

Answers can be found in Part IV.

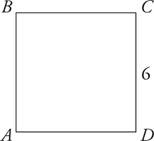
a.What is the area of square ABCD above?

b.What is the perimeter of square ABCD above?

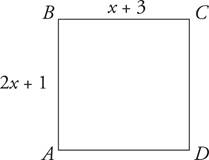
c.If ABCD is a rectangle, x =    y =   

d.What is the perimeter of rectangle ABCD above?

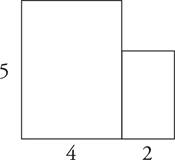
e.If the above figure is composed of two rectangles, what is the perimeter of the figure?

4.If ABCD is a square, what is the area of the square?

A) 2

B) 4

C)20

D)25

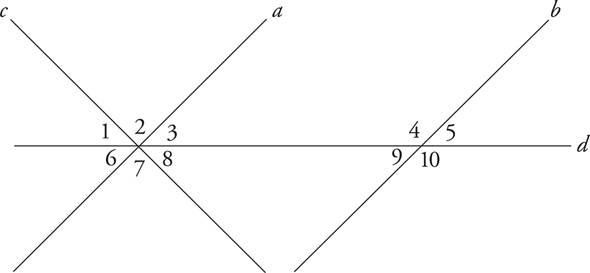
3.In the figure above, lines a and b are parallel. Which of the following pairs of angles must have equal degree measures?

I. 1 and 5

II. 2 and 7

III. 3 and 9

A)I only

B)II only

C)III only

D)II and III only

28.The diagonal of rectangle ABCD is 13 inches long. What is the area of rectangle ABCD?

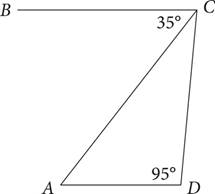
9.In the figure above, BC || AD. What is the measure of ∠ACD?

A)35

B)40

C)50

D)55

TRIANGLES

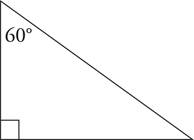
The sum of the angles inside a triangle must equal 180 degrees. This means that if you know two of the angles in a triangle, you can always solve for the third. Since you know that two of the angles in the following figure are 90 and 60 degrees, you can solve for the third angle, which must be 30 degrees. (Note: The little square in the bottom corner of the triangle indicates a right angle, which is 90°.)

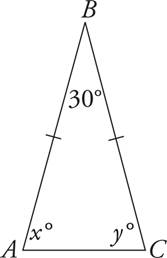
An isosceles triangle has two sides that are equal. Angles that are opposite equal sides must be equal. The figure below is an isosceles triangle. Since AB = BC, you know that angles x and y are equal. And since their sum must be 150 degrees (to make a total of 180 degrees when you add the last angle), they each must be 75 degrees.

The area of a triangle is base × height. Note that the height is always perpendicular to the base.

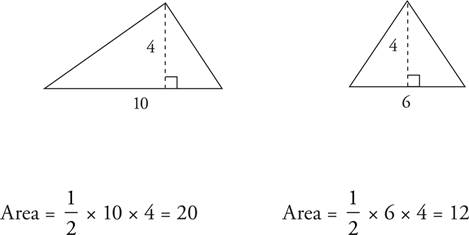
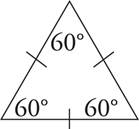
An equilateral triangle has all three sides equal and all of its angles equal to 60 degrees.

Here’s a typical example of a PSAT question on triangles.

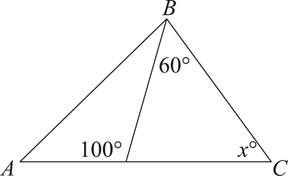
5.In triangle ABC above, what is the value of x?

A)30

B)40

C)50

D)60

Here’s How to Crack It

The question asks for the value of x, which is an angle measure in a triangle. We know that the angle adjacent to the 100° angle must equal 80° since we know that a straight line is 180°. Fill it in on your diagram. Now, since we know that the sum of the angles contained in a triangle must equal 180°, we know that 80 + 60 + x = 180, so x = 40. That’s (B).

Being Aggressive on Geometry Questions

The most important problem-solving technique for tackling PSAT geometry is to learn to be aggressive. This means, whenever you have a diagram, ask yourself What else do I know? Write everything you can think of on your booklet. You may not see right away why it’s important, but write it down anyway. Chances are good that you will be making progress toward the answer, without even knowing it.

The PSAT is also fond of disguising familiar figures within more complex shapes by extending lines, overlapping figures, or combining several basic shapes. So be on the lookout for the basic figures hidden in complicated shapes.

The Pythagorean Theorem

Whenever you have a right triangle, you can use the Pythagorean Theorem. The theorem says that the sum of the squares of the legs of the triangle (the sides that form the right angle) will equal the square of the hypotenuse (the side opposite the right angle).

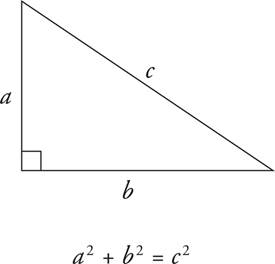
Two of the most common ratios of sides that fit the Pythagorean Theorem are 3-4-5 and 5-12-13. Since these are ratios, any multiples of these numbers will also work, such as 6-8-10 and 30-40-50.

Try the following example.

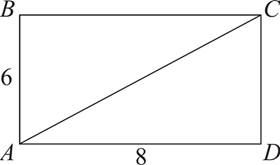
14.If ABCD is a rectangle, what is the perimeter of triangle ABC?

Here’s How to Crack It

The question asks for the perimeter of triangle ABC based on the figure. We can use the Pythagorean Theorem to figure out the length of the diagonal of the rectangle—since it has sides 6 and 8, its diagonal must be 10. (If you remembered that this is one of those well-known Pythagorean triples, you didn’t actually have to do the calculations.) Therefore, the perimeter of the triangle is 6 + 8 + 10, or 24.

Special Right Triangles

There are two specific right triangles, the properties of which may play a role in some harder PSAT math questions. They are the right triangles with angles 45°-45°-90° and 30°-60°-90°. These triangles appear at the front of each Math section, so you don’t have to memorize them.

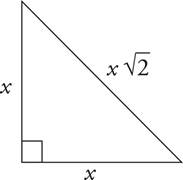
An isosceles right triangle has angles that measure 45, 45, and 90 degrees. Whenever you have a 45°-45°-90° triangle with sides of x, the hypotenuse will always be x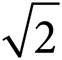. This means that if one of the legs of the triangle measures 3, then the hypotenuse will be .

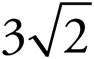This right triangle is important because it is half of a square. Understanding the 45°-45°-90° triangle will allow you to easily find the diagonal of a square from its side, or find the side of a square from its diagonal.

Here’s an example.

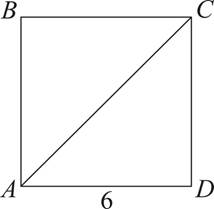
7.In square ABCD above, what is the perimeter of triangle ABC?

A)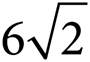

B)8

C)12 +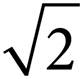

D)12 +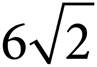

Here’s How to Crack It

The question asks for the perimeter of triangle ABC based on the figure. This question looks like a question about a square, and it certainly is in part, but it’s really more about the two triangles formed by the diagonal.

In this square, we know that each of the triangles formed by the diagonal AC is a 45°-45°-90° right triangle. Since the square has a side of 6, using the 45°-45°-90° right triangle rule, each of the sides is 6 and the diagonal is 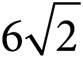. Therefore, the perimeter of the triangle is 6 + 6 + 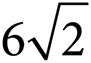, or 12 + 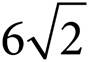and the answer is (D).

The other important right triangle to understand is the 30°-60°-90° right triangle.

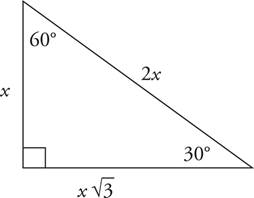
A 30°-60°-90° triangle with a short side of x will have a hypotenuse of 2x and a middle side of 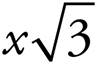. If the smallest side (the x side) of the triangle is 5, then the sides measure 5, 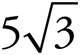, and 10. This triangle is important because it is half of an equilateral triangle, and it allows us to find the height of an equilateral triangle, which is what we’ll need to find the area of an equilateral triangle.

Try the following.

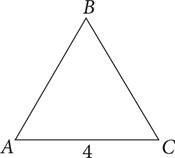
13.Triangle ABC above is equilateral, with sides of length 4. What is its area?

A)3

B)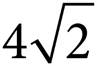

C)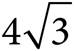

D)8

Triangle Tip

An easy way to figure out the height of an equilateral triangle is to take half of its side and multiply it by the square root of 3.

Here’s How to Crack It

The question asks for the area of an equilateral triangle with a given side length. To find the area of the triangle, we need to know the base and the height. The question tells you that the base AC is 4; now we need to find the height, which is perpendicular to the base. You can create the height by drawing a line from angle B straight down to the base. Now you have two 30°-60°-90° triangles, and you can use the rules of 30°-60°-90° triangles to figure out the height. Half of the base would be 2, and that’s the side across from the 30° angle, so you would multiply it by 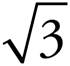to get the height.

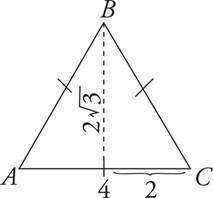
Now we know that the base is 4 and the height is 2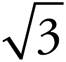, so when we plug those numbers into the formula for area of a triangle, we get A = × 4 × 2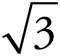, which equals 4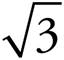. Thus, (C) is the correct answer.

SOHCAHTOA

Trigonometry will likely appear on your PSAT. But fear not! Many trigonometry questions you will see mostly require you to know the basic definitions of the three main trigonometric functions. SOHCAHTOA is a way to remember the three functions:

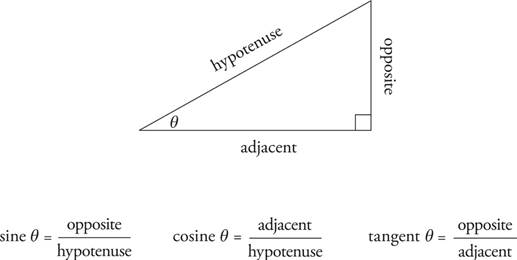
SOHCAHTOA Stands for:

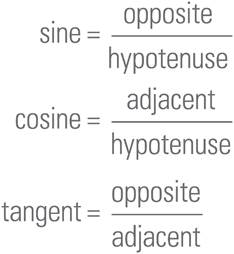
Let’s see an example.

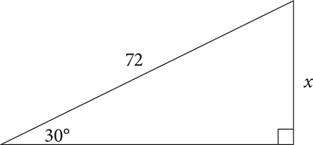
11.Which of the following gives the value of x?

A)72 sin30°

B)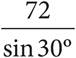

C)72 cos30°

D)72 tan30°

Here’s How to Crack It

The question asks for the value of x, which is a leg on a right triangle. You know the hypotenuse of the triangle, and you want to find the side opposite the 30° angle. SOHCAHTOA tells you that sine is 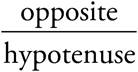, so you want sine. You can eliminate (C) and (D), which do not contain sine. Next, set up the equation using the definition of sine: 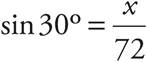. To solve for x, multiply both sides by 72 and you get 72 sin30° = x. This matches (A).

Similar Triangles

Similar triangles have the same shape, but they are not necessarily the same size. Having the same shape means that the angles of the triangles are identical and that the corresponding sides have the same ratio. Look at the following two similar triangles:

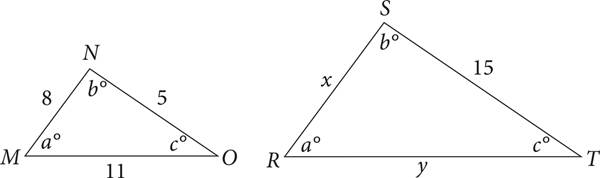
These two triangles both have the same set of angles, but they aren’t the same size. Whenever this is true, the sides of one triangle are proportional to those of the other. Notice that sides NO and ST are both opposite the angle that is a°. These are called corresponding sides, because they correspond to the same angle. So the lengths of NO and ST are proportional to each other. In order to figure out the lengths of the other sides, set up a proportion: 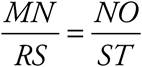. Now fill in the information that you know: 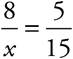. Cross-multiply and you find that x = 24. You could also figure out the length of y: 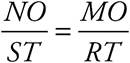. So, 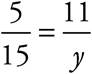, and y = 33. Whenever you have to deal with sides of similar triangles, just set up a proportion.

Give it a try.

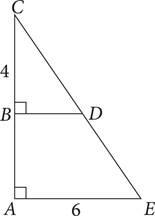
Note: Figure not drawn to scale.

29.If the area of triangle ACE is 18, what is the area of triangle BCD?

Here’s How to Crack It

The question asks for the area of triangle BCD. The formula to find the area of a triangle is A = bh. Plugging in the area and base of triangle ACE as given in the question and the figure gives you the equation 18 = (6)h. Simplify the fraction and you will get 18 = 3h. Divide both sides by 3 and you can see that the height of triangle ACE is 6. Because triangle ACE and triangle BCD have the same angle measures, they are similar. Therefore, you should create a proportion to find the length of BD. The proportion should look like this: 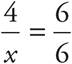, if x represents the length of BD. Simplify your fractions and cross-multiply to see that x = 4. Plug the base and height of triangle BCD into the area formula: A = (4)(4). Simplify the equation and you will see that the area of triangle BCD is 8.

Drill 2

Click here to download a PDF of Chapter 14 Drill 2.

Answers can be found in Part IV.

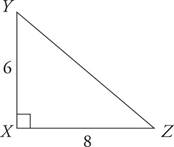
a.What is the area of triangle XYZ above?

b.What is the length of YZ?

c.What is the sine of ∠Z?

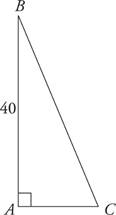
d.If the area of the triangle above is 400, what is the length of AC?

e.What is the length of BC?

f.What is the cosine of ∠C?

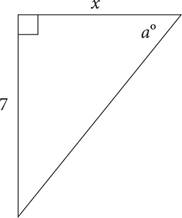
28.In the triangle above, 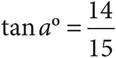. What is the value of x?

Note: Figure not drawn to scale.

14.In triangle ABC above, if AB = BC, what is the value of x? (Disregard the degree symbol when gridding your answer.)

Note: Figure not drawn to scale.

8.In the figure above, if triangle ABC is isosceles, what is the perimeter of the triangle?

A)12.5

B)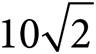

C)

D)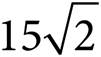

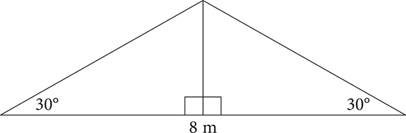
9.The owner of a barn needs to paint the front of the barn’s roof. As shown in the figure above, the roof measures 8 m along the bottom, and the sides of the roof meet the bottom at a 30° angle. If one bucket of paint can cover 5 m2, what is the minimum number of buckets the owner needs to purchase?

A)1

B)2

C)3

D)4

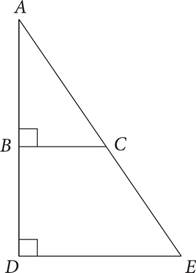
Note: Figure not drawn to scale.

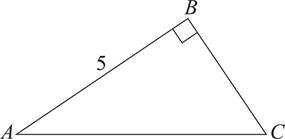
10.In the figure above, if AB = 5, AC = 13, and DE = 24, what is the value of BD?

A)12

B)10

C) 8

D) 5

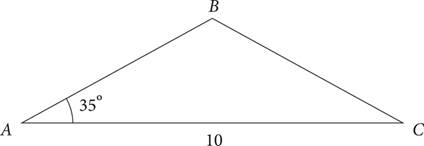
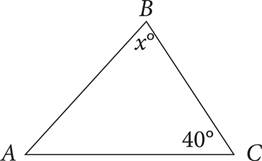
13.In the triangle above, AB = BC. Which of the following accurately expresses the perimeter of the triangle?

A)10 + 10 sin 55°

B)10 + 10 cos 35°

C)10 +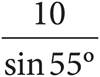

D)25 tan 35°

CIRCLES

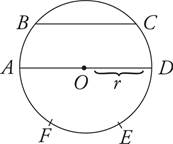
The radius of a circle is the distance from the center to the edge of the circle. In the figure above, OD is a radius. So is OA.

The diameter is the distance from one edge, through the center, to the other edge of the circle. The diameter will always be twice the measure of the radius and will always be the longest line you can draw through a circle. In the figure above, AD is a diameter.

A chord is any line drawn from one point on the edge of the circle to the other. In the figure above, BC is a chord. A diameter is the longest chord in a circle.

An arc is any section of the circumference (the edge) of the circle. is an arc in the figure above.

The circumference is the distance around the outside edge of the circle. The circumference of a circle with radius r is 2πr. A circle with radius of 5 has a circumference of 10π.

The area of a circle with radius r is πr2. A circle with a radius of 5 has an area of 25π.

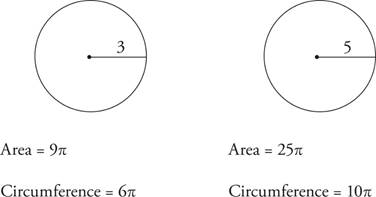
Proportionality in a Circle

Here’s another rule that plays a role in more advanced circle questions.

Arc measure is proportional to interior angle measure, which is proportional to sector area.

Quick Review

· An interior angle is an angle formed by two radii.

· A sector is the portion of the circle between the two radii.

This means that whatever fraction of the total degree measure is made up by the interior angle, the arc described by that angle is the same fraction of the circumference, and the pie piece created has the same fraction of the area.

Take a look at the figure below.

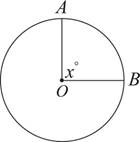
If angle x is equal to 90 degrees, which is one-quarter of 360 degrees, then arc 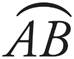is equal to one-quarter of the circumference of the circle and the area of the sector of the circle enclosed by radii OA and OB is equal to one-quarter of the area of the circle.

To see how this works, try the following question.

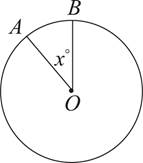
6.The circle above with center O has a radius of 4. If x = 30, what is the length of minor arc AB?

A)

B)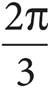

C)3

D)

Here’s How to Crack It

The question asks for the length of minor arc AB. Since the interior angle x is equal to 30°, which is of 360°, we know that minor arc AB will be equal to of the circumference of the circle. Since the circle has radius 4, its circumference will be 8π. Therefore, arc AB will measure 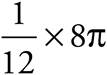, or , (B).

11.Points A and B lie on a circle with center O such that the measure of ∠OAB is 45°. If the area of the circle is 64π, what is the perimeter of ΔAOB?

A) 8 + 8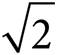

B)16 + 8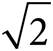

C)16 + 16

D)32 + 16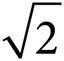

Here’s How to Crack It

The question asks for the perimeter of triangle AOB. This time a diagram isn’t given, so drawing the circle should be your first step. Since points A and B lie on the circle, 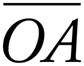and 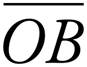are both radii and equal in length, making ΔAOB isosceles. The question indicates that ∠OAB is 45°, which means that ∠OBA is also 45°, which makes ΔAOB a 45°-45°-90° triangle (remember those special right triangles?).

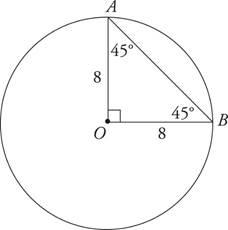
Given the circle’s area of 64π, the radii of the circle (which are the legs of the isosceles right triangle) are 8 and the hypotenuse is 8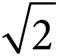, making the perimeter 8 + 8 + 8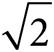, or 16 + 8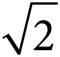, which is (B).

Tangents to a Circle

A tangent is a line that touches the edge of a circle at exactly one point. A radius drawn to the point of tangency forms a 90-degree angle with the tangent line. This comes up occasionally on hard questions, so take a look at the example below. As you work through this question, if you’re thinking that you’d never know how to do it yourself, there’s still a valuable lesson here, and it’s that this question is not in your POOD, so you should look instead for a plug-in or something you’re more familiar with.

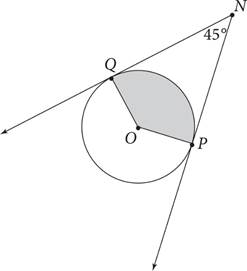
27.In the figure above, NP and NQ are tangent to the circle with center O at points P and Q, respectively. If the area of the shaded region is 24 π, what is the circumference of the circle?

A) 8π

B)12π

C)16π

D)40π

Here’s How to Crack It

The question asks for the circumference of the circle. The key is remembering that any line or line segment drawn tangent to a circle is perpendicular to a radius drawn from the center of the circle to that tangent point; this means both ∠OQN and ∠OPN equal 90°. With ∠QNP given as 45°, that leaves the central ∠QOP of quadrilateral QNPO. Since all quadrilaterals contain 360° and the three angles mentioned so far account for 90 + 90 + 45 = 225°, that remaining angle must be 360 − 225 = 135°. As all circles contain 360° of arc, this means the shaded area represents 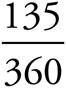, or , of the area of the entire circle.

Remember, we want to write down the formulas for quantities the question talks about, so that’s and . So far we don’t have anything we can put directly into a formula, so what do we know? We’re told that the area of the shaded sector is 24π, so we can use that to figure out the area of the whole circle, because we know it’s proportional to the central angle. In fact, we’ve figured out that this part of the circle is of the whole, so the proportion looks like this: 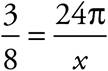. Cross-multiply to get 3x = 192π, then divide both sides by 3 to get x = 64π. Now we can use the first formula and solve for r = 8. We can put this right into the second formula and get , so the answer is (C).

The Equation of a Circle

One last thing you may need to know about a circle is what the equation of a circle in the xy-plane looks like.

The equation of a circle is as follows:

(x − h)2 + (y − k)2 = r2

In the circle equation, the center of the circle is the point (h, k), and the radius of the circle is r.

Let’s look at one.

13.What is the equation of a circle with center (2, 4) that passes through the point (−6, −2)?

A)(x + 2)2+ (y + 4)2 = 100

B)(x + 2)2 + (y + 4)2 =

C)(x − 2)2 + (y − 4)2 = 100

D)(x − 2)2 + (y − 4)2 =

Here’s How to Crack It

The question asks for the equation of a circle with a given center and containing a certain point. Take the given center and put it into the circle equation above. Plugging in h = 2 and k = 4, you get (x − 2)2 + (y − 4)2 = r2. In the circle equation, x and y are the coordinates of a point on the circle. Plugging in the point (−6, −2), you get (−6 − 2)2 + (−2 − 4)2 = r2, which simplifies to (−8)2 + (−6)2 = r2, or 64 + 36 = r2. This means r2 = 100, so the equation is (x − 2)2 + (y − 4)2 = 100. The correct answer is (C).

There is a chance that you might see a circle equation that is not in the form shown above. If this happens, you will need to complete the square to get the given equation into the proper form. Just follow the steps listed for completing the square in the Quadratic Equations section of the previous chapter. The only difference is that you’ll have to do it twice—for the x-terms and for the y-terms. You may decide, however, that such a question is not worth your time. In that case, move on to something else!

Drill 3

Click here to download a PDF of Chapter 14 Drill 3.

Answers can be found in Part IV.

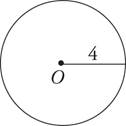
a.What is the area of the circle above with center O?

b.What is its circumference?

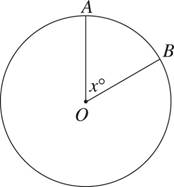
16.The circle shown above has its center at O. If x = 60 and the length of minor arc AB is 2π, what is the area of circle O?

A)36π

B)12π

C) 6π

D) 6

18.A circle with center O has diameter AB. Segment AC is tangent to the circle at point A and has a length of 5. If the area of the circle is 36π, what is the perimeter of triangle ABC?

A)15

B)25

C)30

D)60

12.What is the center of a circle with equation x2 + y2 − 2x + 8y + 8 = 0?

A)(−1, 4)

B)(1, −4)

C)(−2, 8)

D)(2, −8)

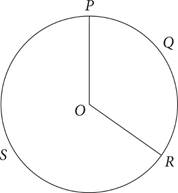
Note: Figure not drawn to scale.

29.Major arc PSR is the length of minor arc PQR. The length of major arc PSR is 6π units. What is the radius of the circle?

VOLUME

Volume questions on the PSAT can seem intimidating at times. The PSAT sometimes gives you questions featuring unusual shapes such as pyramids and spheres. Luckily, at the beginning of the Math sections (and the beginning of this chapter), you’re given a reference information box with all the formulas you will ever need for volume questions on the PSAT.

Let’s look at an example.

15.A sphere has a volume of 36π. What is the surface area of the sphere? (The surface area of a sphere is given by the formula A = 4πr2.)

A) 3π

B) 9π

C)27π

D)36π

Here’s How to Crack It

The question asks for the surface area of a sphere with a given volume. Start by writing down the formula for the volume of a sphere from the beginning of the chapter: 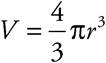. Put what you know into the equation: 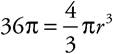. From this you can solve for r. Divide both sides by π to get 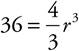. Multiply both sides by 3 to clear the fraction: 36(3) = 4r3. Note that we left 36 as 36 because the next step is to divide both sides by 4, and 36 divided by 4 is 9, so 9(3) = r3 or 27 = r3. Take the cube root of both sides to get r = 3. Now that you have the radius, use the formula provided to find the surface area: A = 4π(3)2, which comes out to 36π, (D).

PLUGGING IN ON GEOMETRY

You can also use Plugging In on geometry questions, just as you can for algebra. Any time that you have variables in the answer choices or hidden variables, use Plugging In! As long as you follow all the rules of geometry while you solve, you’ll get the answer.

Take a look at this question.

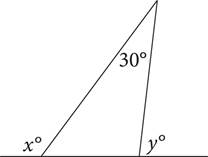
8.In the figure above, what is the value of x + y?

A)140

B)180

C)190

D)210

Here’s How to Crack It

The question asks for the value of x + y, which are two angle measures on a figure. You could answer this question using algebra, but why? You can plug in whatever numbers you want for the other angles inside the triangle—as long as you make sure that all the angles in the triangle add up to 180°. So plug in 60 and 90 for the other angles inside that triangle. Now you can solve for x and y: if the angle next to x is 60°, then x will be equal to 120. If the angle next to y is equal to 90°, then y will be equal to 90. This makes the sum x + y equal to 120 + 90, or 210. No matter what numbers we pick for the angles inside the triangle, we’ll always get the same answer, (D).

Drill 4

Click here to download a PDF of Chapter 14 Drill 4.

Try to use Plugging In on the following questions. Answers can be found in Part IV.

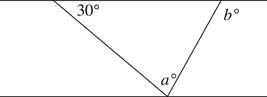
3.In the figure above, what is the value of b, in terms of a?

A)30 − a

B)30 + a

C)60 + a

D)80 − a

7.Cone A and Cone B are both right circular cones with the same height. If the radius of Cone A is of the radius of Cone B, which of the following is the ratio of the volume of Cone A to the volume of Cone B?

A)27:64

B) 9:16

C) 3:4

D) 4:3

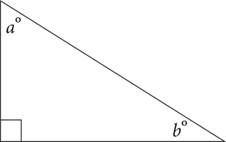
5.If sin ao = x, then cos bo =

A)x

B)1 − x

C)

D)x − 1

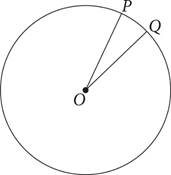
22.In the figure above, O is the center of the circle, the radius of the circle is x, and the length of minor arc PQ is 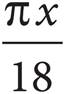. What is the area of sector POQ?

A)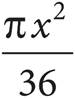

B)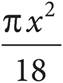

C)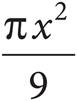

D)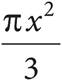

26.Three spherical balls with radius r are contained in a rectangular box. Two of the balls are each touching 5 sides of the rectangular box and the middle ball. The middle ball also touches four sides of the rectangular box. What is the volume of the space between the balls and the rectangular box?

(Note: The volume of a rectangular solid is given by the equation V = lwh. The volume of a sphere is given by the equation V = πr3).

A)r3(3 − 4π)

B)4r2(14 − π)

C)4r3(6 − π)

D)12r2(r − π)

29.A rectangular box is half as long as it is wide and one-third as wide as it is tall. If the volume of the box is 96, then what is its surface area? (Note: The formula for the volume of a rectangular solid is V= lwh.)

IMAGINARY AND COMPLEX NUMBERS

So far you have been working with real numbers, which are any numbers that you can place on a number line. The PSAT may ask you to do mathematical operations with imaginary or complex numbers.

An imaginary number, very simply, is the square root of a negative number. Since there is no way to have a real number that is the square root of a negative number, mathematicians needed to come up with a way to represent this concept when writing equations. They use an italicized lowercase “I” to do that: i = , and the PSAT will likely tell you that in any question involving imaginary numbers.

A complex number is one that has a real component and an imaginary component connected by addition or subtraction. 8 + 7i and 3 − 4i are two examples of complex numbers.

You may be tested on complex numbers in a variety of ways. You may be asked to add or subtract the complex numbers. When you are completing these operations, you can treat i as a variable. Just combine the like terms in these expressions and then simplify. (Don’t forget to distribute the subtraction sign.)

Here is an example.

7.If i = , which of the following is equivalent to (4 + 3i) − (2 − 2i)?

A)3

B)2 + i

C)6 + i

D)2 + 5i

Here’s How to Crack It

The question asks for an expression equivalent to one containing complex numbers. Start by distributing the negative sign: (4 + 3i) − (2 − 2i) = 4 + 3i) − 2 + 2i. Be careful with the negative signs, which are often the trickiest part of imaginary number questions. The real parts are 4 and − 2, which can be added together to get 2. The imaginary parts are 3i and 2i. These can also be added together to get 5i. Note you cannot combine real parts and imaginary parts in a complex number, so the answer is simply (D).

The PSAT may also ask you to multiply complex numbers. Again, you can treat i as a variable as you work through the multiplication as if you were multiplying binominals. In other words, use FOIL to work through the question. The only difference is that you substitute −1 for i2.

Let’s look at one.

10.If i2 = −1 and a = (i + 6), which of the following is the result of squaring a?

A)36i

B)i + 36

C)12i + 35

D)12i + 36

Here’s How to Crack It

The question asks for the result of squaring a. The question states that a = (i + 6), so the square of a must be (i + 6)2. Expand the squared term using FOIL and you get i2 + 6i + 6i + 36. Combine like terms to get i2 + 12i + 36. Since i2 = −1, you can simplify further to (−1) + 12i + 36, or 12i + 35, which is (C).

Note that this question would appear in the calculator-allowed section. Your calculator has a handy i button, so feel free to use it when allowed if things get tricky.

Summary

o Be sure to review your basic geometry rules before the test; often, questions hinge on knowing that vertical angles are equal or that the sum of the angles in a quadrilateral is 360°.

o On all geometry questions, draw figures out and aggressively fill in everything you know.

o When two parallel lines are cut by a third line, the small angles are equal, the big angles are equal, and the sum of a big angle and a small angle is 180°.

o The perimeter of a rectangle is the sum of the lengths of its sides. The area of a rectangle is length × width.

o The perimeter of a triangle is the sum of the lengths of its sides. The area of a triangle is 1/2 base × height.

o Knowing the Pythagorean Theorem, common Pythagorean triples (such as 3-4-5 and 5-12-13), and special right triangles (45°-45°-90° and 30°-60°-90°) will help you figure out angles and lengths in a right triangle.

o For trigonometry questions, remember SOHCAHTOA:

·   sine = .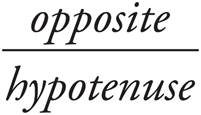

·   cosine = .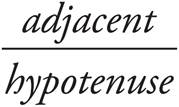

·   tangent = .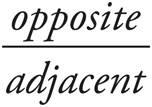

o Similar triangles have the same angles and their side lengths are proportional.

o The circumference of a circle is 2πr. The area of a circle is πr2.

o Circles that show an interior angle (an angle that extends from the center of the circle) have proportionality. The interior angle over the whole degree measure (360°) equals the same fraction as the arc enclosed by that angle over the circumference. Likewise, both of these fractions are equal to the area of the segment over the entire area of the circle.

o When you see a line that is “tangent to” a circle, remember two things:

·   The line touches the circle at exactly one point.

·   The radius of the circle that intersects the tangent line is perpendicular (90°) to that tangent line.

o The formulas to compute the volumes of many three-dimensional figures are supplied in the instructions at the front of both Math sections.

o When plugging in on geometry questions, remember to use your knowledge of basic geometry rules; e.g., there are still 180° in a triangle when you’re using Plugging In.

o The imaginary number i = 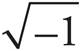. When doing algebra with i, treat it as a variable, unless you are able to substitute −1 for i2 when appropriate.